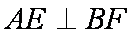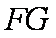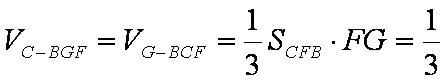- 导数与积分
- 共3028题
执行如图所示的程序框图,若输出的

正确答案
解析
由程序框图可知:
①







⑤




知识点
函数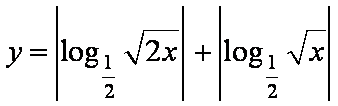
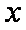
正确答案
解析
略
知识点
一艘船上午9:30在A处,测得灯塔S在它的北偏东300处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东750,且与它相距8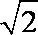
正确答案
解析
经计算∠A=30°,∠S=45°,AB=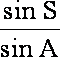
知识点
如图,有两座建筑物AB和CD都在河的对岸(不知 道它们的高度,且不能到达对岸),某人想测量两 座建筑物尖顶A、C之间的距离,但只有卷尺和测 角仪两种工具.若此人在地面上选一条基线EF,用 卷尺测得EF的长度为a,并用测角仪测量了一些角度:




正确答案
见解析
解析
解析:第一步:在

解得
第二步:在

第三步:在
…………12分
知识点
已知抛物线



正确答案
解析
设




联立直线与抛物线方程消去


故
知识点
直线



正确答案
解析
由








解得n=2
又直线y=5截曲线的弦长与直线y=-1截曲线的弦长相等且不为0,则可得m>3. 故选D
知识点
已知函数
(1)求f(x)的解析式;
(2)设函数


正确答案
见解析
解析
解析: (1)
由








(2)由(1)知






依题意
(ⅰ)当







(ⅱ)当




















综上,所求

知识点
已知函数



正确答案
5
解析
略
知识点
椭圆
(1)若ΔABF2为正三角形,求椭圆的离心率;
(2)若椭圆的离心率满足
正确答案
见解析
解析
解析:(1)由椭圆的定义知




∴
在


∴椭圆的离心率
(2)设




①当直线









②当直线




整理得:


令



知识点
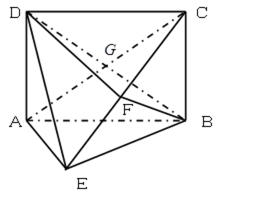
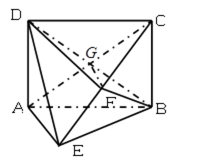
如图所示,矩形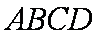
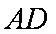
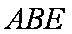
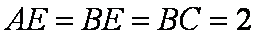
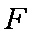
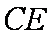
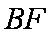
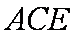
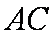
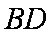

(1)求证: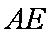
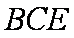
(2)求证: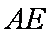
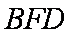
(3)求三棱锥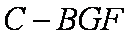
正确答案
见解析。
解析
(1)证明:∵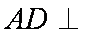
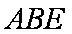
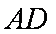
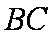
∴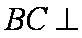
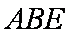

又

∴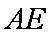
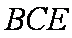
(2)由题意可得
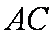
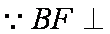
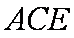

而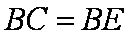
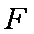
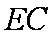
在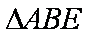
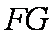
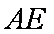
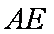
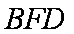
(3)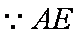
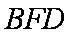
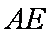
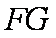
而∴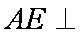
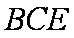
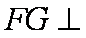
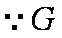
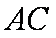

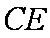
∴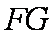
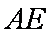
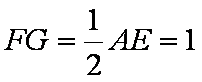
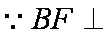
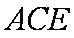

∴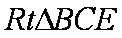
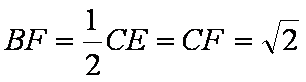
∴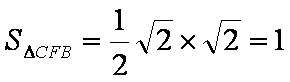
∴
知识点
扫码查看完整答案与解析