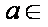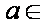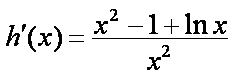- 导数与积分
- 共3028题
已知函数





正确答案
解析
作函数











知识点
如图,在直角三角形




(1)若

(2)试判断
(3)求

正确答案
见解析
解析
(1)[解法1] 


,即




[解法2]将已知方程两边平方,得

即



(2)[解法1]以O为原点,建立平面直角坐标系,设



则由

[解法2]
所以,
(3) [解法1]作




[解法2] 



知识点
已知函数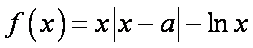
(1)若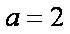
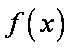
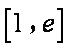
(2)若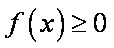
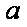
注: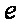
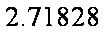
正确答案
见解析
解析
解:(1) 若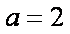
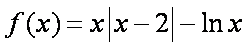
当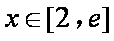
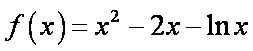

所以函数
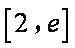
当
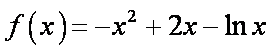
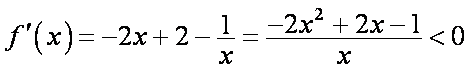
所以函数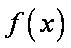
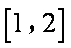
所以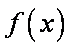
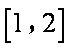
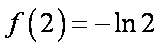
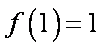
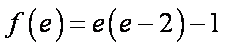
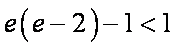
所以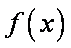
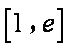
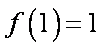
(2) 函数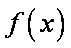
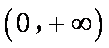
由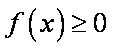
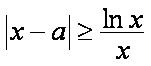
(ⅰ)当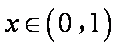
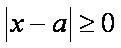
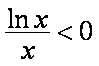
不等式(*)恒成立,所以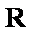
(ⅱ)当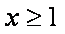
①当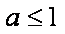
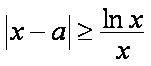
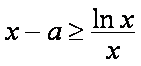
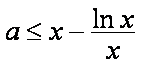
现令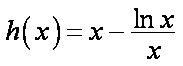
因为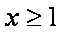
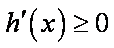
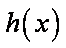
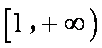
从而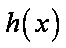
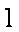
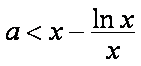
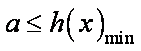
所以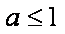
②当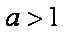
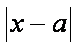
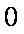
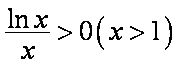
综上可得,满足条件的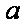
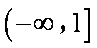
知识点
已知函数f(x)=ex﹣ae﹣x,若f′(x)≥2
正确答案
[3,+∞)
解析
函数的导数f'(x)=ex+ae﹣x,所以由f′(x)≥2


设t=ex,则t>0,则函数

即实数a的取值范围是[3,+∞)。
知识点
已知函数
(1)求函数
(2)若


正确答案
见解析
解析
(1)

由


∴函数


(2)∵


∵


∴
知识点
已知函数
(1)若函数


(2)在(1)的条件下,对任意



(3)若





正确答案
见解析
解析
(1)
(2)由(1)知,
故
(3)
则
①若


②若






知识点
如图,在三棱锥





(1)求证:
(2)设点



正确答案
见解析
解析
证明:(1)方法一:由


又


故
同理可得


则

方法二:由已知可得












(2)方法一:由(1)的证明过程知







由已知可得



又

故


方法二: 由(I)的证明过程知
标系,则
可得

的一个法向量为




则


知识点
如图,在△




















(1)求证:

(2)设



正确答案
见解析
解析
(1)因为




因为平面




同理,




所以平面



(2)以C为原点,





则






平面

平面

由
化简得

知识点
已知函数f(x)=log2

正确答案
解析
解:∵已知函数f(x)=log2


故函数f(x) 是奇函数,则f(﹣a)=﹣f(a)=﹣
故选 D。
知识点
在△ABC中,角A,B,C的对边分别为a,b,c,且
(1)求角B的大小;
(2)已知

正确答案
见解析
解析
解:(1)

∵

∴


(2)

∴


而
∴

知识点
扫码查看完整答案与解析