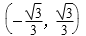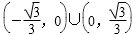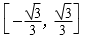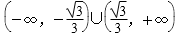导数与积分
共3028题

导数与积分
共3028题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

21.已知函数，（其中常数）

（1）当时，求的极大值；

（2）试讨论在区间上的单调性；

（3）当时，曲线上总存在相异两点、，使得曲线在点、处的切线互相平行，求的取值范围.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

7．已知函数在R上满足，则曲线在点处的切线方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

12.如果方程有解，则实数的取值范围是________.

正确答案

或≤

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

21.已知数列的各项均为正值，对任意，都成立.

（1）求数列、的通项公式；

（2）令，求数列的前项和;

（3）当且时，证明对任意都有成立.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

9．若曲线C1：x2＋y2－2x＝0与曲线C2：y(y－mx－m)＝0有4个不同的交点，则实数m的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

1.的值等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

简答题 · 13 分

21．对于函数，若存在，使成立，则称为的不动点．如果函数有且仅有两个不动点0，2，且．

（1）求函数的单调区间；

（2）已知数列各项不为零且不为1，满足，求证：；

（3）设，为数列的前项和，求证：

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

填空题 · 5 分

9.设复数满足=，则=____________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

单选题 · 4 分

17．对于数列，若存在常数，使得对任意，与中至少有一个不小于，则记作，那么下列命题正确的是（）

A若，则数列各项均大于或等于

B若，则

C若，，则

D若，则

正确答案

解析

（A）的反例可以是:，．（B）的反例可以是:，．

（C）的反例可以是:和，．

知识点

导数的加法与减法法则

题型：简答题

简答题 · 18 分

23．已知抛物线上任意一点到焦点的距离比到轴的距离大1

（1）求抛物线的方程；

（2）若过焦点的直线交抛物线于两点，在第一象限，且，求直线的方程；

（3）求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题。

例如，原来问题是“若正四棱锥底面边长为，侧棱长为，求该正四棱锥的体积”。求出体积后，它的一个“逆向”问题可以是“若正四棱锥底面边长为，体积为，求侧棱长”；也可以是“若正四棱锥的体积为，求所有侧面面积之和的最小值”。

现有正确命题:过点的直线交抛物线于两点，设点关于轴的对称点为，则直线必过焦点。

试给出上述命题的“逆向”问题，并解答你所给出的“逆向”问题。

正确答案

（1）．

（2）设，则，F（1，0）

因为M、F、N共线，则有，所以，解得，

所以，因而，直线的方程是

（3）“逆向问题”一：

①已知抛物线C：的焦点为F，

过点F的直线交抛物线C于P、Q两点，

设点P关于x轴的对称点为R，

则直线RQ必过定点

证明：设过F的直线为y=k（x），，，

则

由

得，

所以，

，

=，

所以直线RQ必过焦点A。

②过点的直线交抛物线C于P、Q两点，FP与抛物线交于另一点R，则RQ垂直于x轴。

③已知抛物线C：，过点B（m，0 ）（m>0）的直线交抛物线C于P、Q两点，设点P关于x轴的对称点为R，则直线RQ必过定点A（-m，0）。

“逆向问题”二：

已知椭圆C：的焦点为F1（-c，0），F2（c，0），过F2的直线交椭圆C于P、Q两点，设点P关于x轴的对称点为R，则直线RQ必过定点。

“逆向问题”三：

已知双曲线C：的焦点为F1（-c，0），F2（c，0），过F2的直线交双曲线C于P、Q两点，设点P关于x轴的对称点为R，则直线RQ必过定点

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 导数与积分

扫码查看完整答案与解析