导数与积分
共3028题

导数与积分
共3028题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

7．直线与双曲线的右支交于不同两点，则k的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

简答题 · 14 分

20．某自来水厂的蓄水池存有400吨水，水厂每小时可向蓄水池中注水60吨，同时蓄水池又向居民小区不间断供水，小时内供水总量为吨，（）

（1）从供水开始到第几小时时，蓄水池中的存水量最少？最少水量是多少吨?

（2）若蓄水池中水量少于80吨时，就会出现供水紧张现象，请问：在一天的24小时内，有几小时出现供水紧张现象。

正确答案

（1）设小时后蓄水池中的水量为吨，则；

令＝；则，即；

∴当，即时，，即从供水开始到第6小时时，蓄水池水量最少，只有40吨。

（2）依题意，得，解得，，即

，；由，所以每天约有8小时供水紧张。

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

8. 设则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

简答题 · 16 分

21．设有唯一解，已知．

（1）求数列{xn}的通项公式；

（2）若，求和：Sn=b1+b2+…+bn；

（3）是否存在最小整数m，使得对任意n∈N*，有成立，若存在，求出m的值，若不存在，说明理由．

正确答案

（1）因方程f（x）=x有唯一解，可求a=从而得到．

数列{}是首项为，公差为的等差数列，

故=，

所以数列{xn}的通项公式为．

（2）将xn代入an可求得an=2n－1，所以．

（3）恒成立，

即要，故存在最小的正整数m=3．

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

19．如图，扇形AOB，圆心角AOB等于60°，半径为2，在弧AB上有一动点P，过P引平行于OB的直线和OA交于点C，设∠AOP＝θ，求△POC面积的最大值及此时θ的值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

21．已知函数，x∈R(ω>0)，在y轴右侧的第一个最高点的横坐标为．

（1）求ω；

（2）若将函数f(x)的图象向右平移个单位后，再将得到的图象上各点横坐标伸长到原来的4倍，纵坐标不变，得到函数y＝g(x)的图象，求函数g(x)的最大值及单调递减区间．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

填空题 · 4 分

9．在的展开式中，的系数是和的系数的等差中项，若实数，那么（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

填空题 · 4 分

8．在△ABC中三边之比a:b:c=2:3:，则△ABC中最大角= （）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

简答题 · 12 分

21．已知函数．

（1）函数在区间上是增函数还是减函数？证明你的结论；

（2）当时，恒成立，求整数的最大值；

（3）试证明：（）。

正确答案

解：（Ⅰ）由题

故在区间上是减函数;

（Ⅱ）当时，恒成立，即在上恒成立，取，则，

再取则

故在上单调递增，

而，

故在上存在唯一实数根，

故时，时，

故故

以①式代入可得AB的斜率k=为定值；

（3）由（2）知：

令，

又

即：

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

单选题 · 5 分

8．若，当，时，，若在区间，内有两个零点，则实数的取值范围是（）

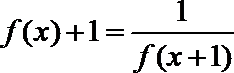
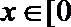
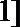
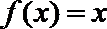
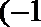
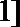
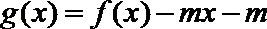
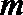
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 导数与积分

扫码查看完整答案与解析