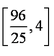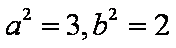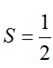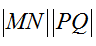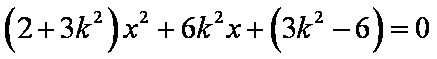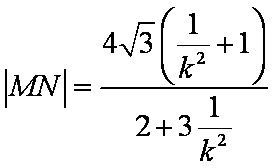- 椭圆及其性质
- 共751题
已知椭圆C的左、右焦点分别为


(1)求椭圆C的标准方程;
(2)线段




正确答案
见解析
解析
(1)

(2)显然直线

当直线




当直线



整理,得

令
所以
由上,得
所以当直线


设

即



所以,
知识点
已知椭圆







(1)求椭圆
(2)设椭圆






正确答案
见解析
解析
(1)当

所以:
解得:
所以椭圆方程是:
(2)当








证明如下:设点M,N点的坐标分别是


所以点



由方程组

所以:
从而:
所以:以


知识点
已知椭圆




(1)求椭圆
(2)设直线的







正确答案
见解析
解析
解析:(1)因为以坐标原点为圆心,椭圆短轴长为直径的圆经过椭圆的焦点,所以






可得


(2)直线的




联立方程




从而

知识点
已知椭圆







(1)求椭圆
(2)设椭圆






正确答案
见解析
解析
(1)当


解得:

(2)当








证明如下:设点M,N点的坐标分别是


所以点



由方程组

所以:
从而:
所以:以


知识点
已知某圆锥曲线


(1)试将圆锥曲线
(2)以圆锥曲线
正确答案
见解析。
解析
(1)由方程

(2)曲线


所以曲线
知识点
以



(1)求椭圆
(2)过点










正确答案
见解析
解析
解析: 解法一: (1)设椭圆方程为

又
所以


(2)若直线l与x轴重合,则以AB为直径的圆是x2+y2=1, …………5分
若直线l垂直于x轴,则以AB为直径的圆是(x+

由

因此所求的点T如果存在,只能是(1,0),
事实上,点T(1,0)就是所求的点,证明如下:
当直线l垂直于x轴时,以AB为直径的圆过点T(1,0)。
若直线l不垂直于x轴,可设直线l:y=k(x+
由


记点A(x1,y1),B(x2,y2),则
又因为




=(k2+1)x1x2+(

=(k2+1) 



所以TA⊥TB,即以AB为直径的圆恒过点T(1,0)。
所以在坐标平面上存在一个定点T(1,0)满足条件。…………13分
解法二:(1)由已知

因为点P在椭圆C上,所以

所以椭圆C的方程是:
(2)假设存在定点T(u,v)满足条件。
同解法一得(k2+2)x2+

记点A(x1,y1),B(x2,y2),则
又因为



所以
=(k2+1)x1x2+(


=(k2+1) 




=
当且仅当



当直线l垂直于x轴时,以AB为直径的圆
所以在坐标平面上存在一个定点T(1,0)满足条件,…………13分
解法三:(1)同解法一或解法二。………………4分
(2)设坐标平面上存在一个定点T满足条件,根据直线过x轴上的定点S及椭圆的对称性,所求的点T如果存在,只能在x轴上,设T(t,0),……5分
同解法一得
又因为




=(k2+1)x1x2+(

=(k2+1) 



= 
当且仅当


所以当t=1时,以AB为直径的圆恒过点T。……………………12分
当直线l垂直于x轴时,以AB为直径的圆
所以在坐标平面上存在一个定点T(1,0)满足条件。………………13分
知识点
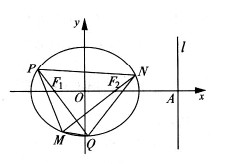
如图,F1、F2分别为椭圆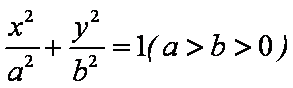
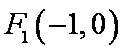
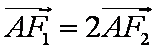
(1)求椭圆的方程;
(2)过F1、F2作互相垂直的两直线分别与椭圆交于P、Q、M、N四点,求四边形PMQN面积的取值范围。
正确答案
(1)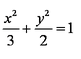
解析
解析:(1)由F1(-1,0)得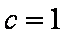
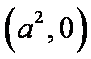
∵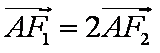
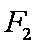
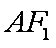
∴ 椭圆方程为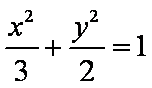
(2)当直线MN与PQ之一与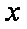
…………6分
当直线PQ,MN均与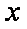
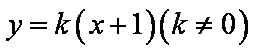
联立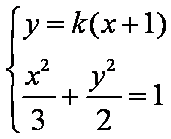
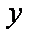
设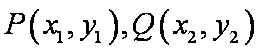
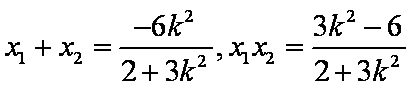
∴ 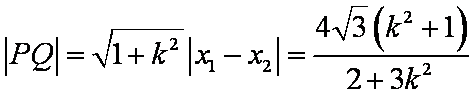
∴四边形PMQN面积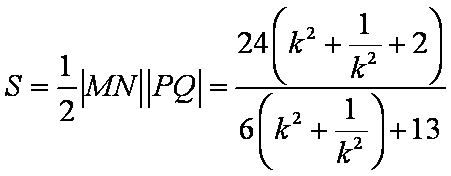
令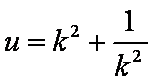
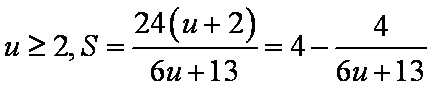
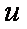
所以当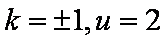

综上可知,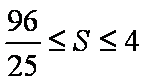
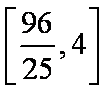
知识点
已知A、B、C是椭圆


(1)求椭圆
(2)过点

正确答案
(1)
解析
解析:(1)∵
则
∴∠OCA=90°, 即
又∵
将C点坐标代入得
解得 c2=8,b2=4
∴椭圆m:
(2)由条件D(0,-2) ∵M(0,t)
①当k=0时,显然-2<t<2 …………6分
②当k≠0时,设


由△>0 可得 
设
则


由
∴
∴t>1 将①代入②得 1<t<4
∴t的范围是(1,4)………………12分
综上t∈(-2,4) ………………13分
知识点
如图,设








(1) 求椭圆的标准方程;
(2) 求证:对于任意的割线

(3) 求三角形△ABF面积的最大值。
正确答案
见解析
解析
解析:(1)∵















∴



(3)





知识点
椭圆
(1)如果点A在圆
(2)若函数

正确答案
(1)
解析
解析:(1)∵点A在圆
由椭圆的定义知:|AF1|+|AF2|=2a,
(2)∵函数
∴
点F1(-1,0),F2(1,0),
①若
∴
②若AB与x轴不垂直,设直线AB的斜率为k,则AB的方程为y=k(x+1)
由

设点A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两个根
由①②知
知识点
扫码查看完整答案与解析