椭圆及其性质_章节学习

1

题型：简答题

|

简答题 · 12 分

21．已知椭圆的离心率为,短轴一个端点到右焦点的距离为．

（Ⅰ）求椭圆的方程；

（Ⅱ）设直线与椭圆交于两点，坐标原点到直线的距离为，求面积的最大值．

正确答案

（Ⅰ）设椭圆的半焦距为，依题意

∴ ，∴ 所求椭圆方程为．

（Ⅱ）设，．

（1）当轴时，．

（2）当与轴不垂直时，设直线的方程为．

由已知，得．

把代入椭圆方程，整理得，

，．

．

当且仅当，即时等号成立．当时，，

综上所述．

所以，当最大时，面积取最大值．

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

1

题型：填空题

|

填空题 · 5 分

14．已知函数的导函数为，且，则的最小值为_____．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

1

题型：填空题

|

填空题 · 5 分

14.已知、分别是椭圆的左、右焦点，点在椭圆上，的平分线交轴于点，则 ________.

正确答案

2

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 12 分

20．已知椭圆经过点，离心率为，直线交椭圆于不同的两点、.

（1）求椭圆的方程

（2）问能否成为以为底边的等腰三角形，若能，求出面积的最大值，若不能，请说明理由。

正确答案

（1）

，

椭圆方程

（2）①当直线l的斜率等于时，设，

则交点A、B关于轴对称，此时，为等腰三角形，

，

到边的距离为，，

构造函数，

则，

令得到，当时，当时，，

②当直线的斜率不为零时，可以设直线为，

，

由于，所以的中垂线经过点，

的中点，

，，化简得到：①

又，即②

由①，②以及得：，无解，

所以，此时以为顶点的等腰三角形不存在.

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

1

题型：填空题

|

填空题 · 4 分

10．已知分别是椭圆的左、右焦点，点是椭圆上的任意一点，则的取值范围是（）．

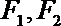
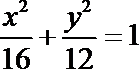
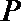
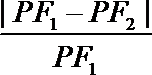
正确答案

[0，2]

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 18 分

22．已知椭圆的左，右两个顶点分别为．，曲线是以．两点为顶点，焦距为的双曲线。设点在第一象限且在曲线上，直线与椭圆相交于另一点。

（1）求曲线的方程；

（2）设．两点的横坐标分别为．，求证为一定值；

（3）设与（其中为坐标原点）的面积分别为与，且，求的取值范围。

正确答案

（1）依题意可得，

双曲线的焦距为，

，

双曲线的方程为

（2）证明：设点、（，），

直线的斜率为（），

则直线的方程为

联立方程组整理，

得

解得或

同理方程组

可得：

为一定值

（3）设点、（，），

则，．

，

即

点在双曲线上，

则，

所以，

即

又点是双曲线在第一象限内的一点，

所以

，

由（2）知，，

即，

设，则，

，

在上单调递减，在上单调递增

当，即时，

的取值范围为

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

1

题型：填空题

|

填空题 · 5 分

15．若函数在上的导函数为，且不等式恒成立，又常数，满足，则下列不等式一定成立的是．

①；

②；

③；

④．

正确答案

①

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

1

题型：单选题

|

单选题 · 5 分

3．“”是“方程表示焦点在轴上的椭圆”的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定椭圆的定义及标准方程

1

题型：简答题

|

简答题 · 13 分

20．已知椭圆C：的一个焦点是（1，0），两个焦点与短轴的一个端点构成等边三角形．

（1）求椭圆C的方程；

（2）过点Q（4，0）且不与坐标轴垂直的直线l交椭圆C于A、B两点，设点A关于x轴的对称点为A1．求证：直线A1B过x轴上一定点，并求出此定点坐标．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程圆锥曲线的定点、定值问题直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 13 分

20．已知椭圆C：＋＝1(a＞b＞0)的离心率e＝，椭圆C的上、下顶点分别为A1，A2，左、右顶点分别为B1，B2,左、右焦点分别为F1，F2．原点到直线A2B2的距离为．

（1）求椭圆C的方程；

（2）过原点且斜率为的直线l，与椭圆交于E，F点，试判断∠EF2F是锐角、直角还是钝角，并写出理由；

（3）P是椭圆上异于A1，A2的任一点,直线PA1，PA2，分别交轴于点N，M,若直线OT与过点M，N的圆G相切，切点为T．证明：线段OT的长为定值,并求出该定值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程圆锥曲线的定点、定值问题圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点