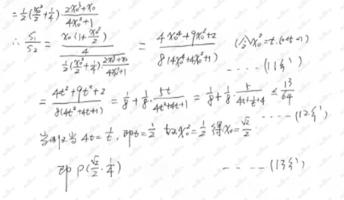- 椭圆及其性质
- 共751题
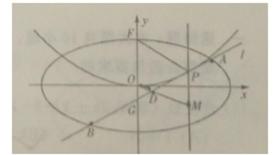
21.(本小题满分14分)
平面直角坐标系
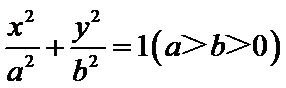
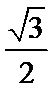
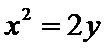
(I)求椭圆C的方程;
(II)设P是E上的动点,且位于第一象限,E在点P处的切线
(i)求证:点M在定直线上;
(ii)直线
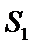
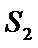
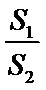
正确答案
知识点
19.设椭圆



(I)求椭圆的方程;
(II)设过点A的直线l与椭圆交于点B(B不在x轴)上,垂直于l的直线与l交于点M,与y轴交于点H.若BF⊥HF,且∠MOA≤∠MAO,求直线l的斜率的取值范围。
正确答案
知识点
7.已知椭圆



正确答案
知识点
设椭圆



(I)求椭圆的方程;
(II)设过点A的直线l与椭圆交于点B(B不在x轴)上,垂直于l的直线与l交于点M,与y轴交于点H.若BF⊥HF,且∠MOA≤∠MAO,求直线l的斜率的取值范围。
正确答案
(1)解:设







(2)(Ⅱ)解:设直线








解得



由(Ⅰ)知,









设










所以,直线
知识点
21.(本小题满分14分)
平面直角坐标系



(I)求椭圆C的方程;
(II)设P是E上的动点,且位于第一象限,E在点P处的切线
(i)求证:点M在定直线上;
(ii)直线



正确答案
(Ⅰ)由题意知

因为抛物线


所以椭圆C的方程为
(Ⅱ)(i)设


所以直线

因此直线


设
得
由


因此
将其代入

因为


联立方程


即点

(ii)由(i)知直线

令


又
所以

所以
令

当





所以点





考查方向
知识点
19.已知椭圆C:

(I)求椭圆C的方程;
(I I)设P是椭圆C上一点,直线PA与Y轴交于点M,直线PB与x轴交于点N。
求证:



正确答案
知识点
20.(本小题满分13分)
已知椭圆E:
(I)求椭圆E的方程及点T的坐标;
(II)设O是坐标原点,直线l’平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数λ,使得∣PT∣2=λ∣PA∣·∣PB∣,并求λ的值.
正确答案
知识点
19.如图,设椭圆C:
(Ⅰ)求直线
(Ⅱ)若任意以点
正确答案
知识点
22.选修4-1:几何证明选讲
如图,⊙O中
(I)若∠PFB=2∠PCD,求∠PCD的大小;
(II)若EC的垂直平分线与FD的垂直平分线交于点G,证明OG⊥CD.
23.选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线



(I)写出

(II)设点P在

24.选修4-5:不等式选讲
已知函数
(I)当a=2时,求不等式
(II)设函数

正确答案
知识点
如图,设椭圆C:
(Ⅰ)求直线
(Ⅱ)若任意以点
正确答案
I)设直线



故


因此

(II)假设圆与椭圆的公共点有




记直线






由(I)知,


故

所以
由于



因此

因为①式关于


所以

因此,任意以点


由

知识点
扫码查看完整答案与解析