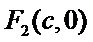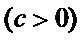- 椭圆及其性质
- 共751题
已知椭圆E: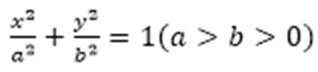
25.求椭圆E的方程及点T的坐标;
26.设O是坐标原点,直线l’平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数λ,使得∣PT∣2=λ∣PA∣·∣PB∣,并求λ的值.
正确答案
(Ⅰ)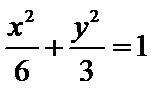
解析
(I)设短轴一端点为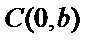
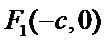
则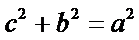
由题意,
∴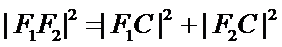
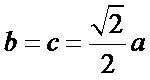
∴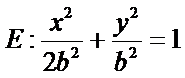
代入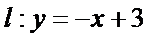
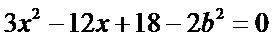
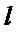
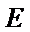
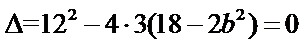
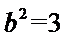
∴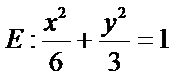
由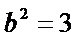
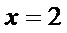
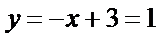
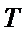
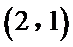
考查方向
解题思路
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题时,一般都设交点坐标为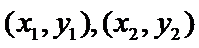
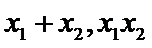
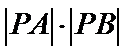
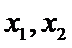

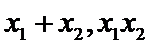
易错点
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.易在第二问运算中出错。
正确答案
(Ⅱ)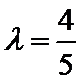
解析
(II)设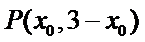
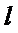
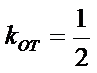
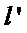
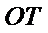
得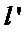
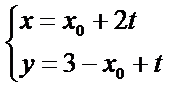
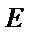
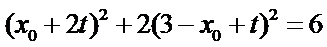
整理可得 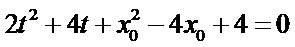
设两根为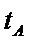
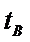
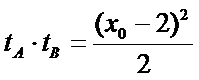
而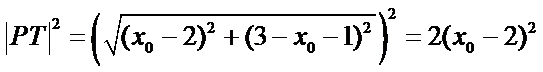
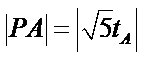
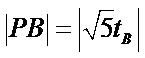
故有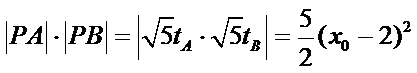
由题意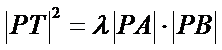
∴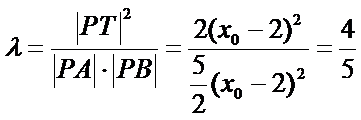
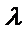
考查方向
解题思路
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题时,一般都设交点坐标为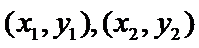
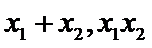
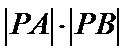
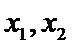

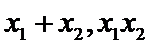
易错点
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.易在第二问运算中出错。
已知椭圆









24.当

25.当

正确答案
(Ⅰ)
解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
(I)设





由已知及椭圆的对称性知,直线



将





因此

因此


考查方向
解题思路
(1)先求出直线AM的方程,再求点M的纵坐标,最后求
易错点
不知如何运用题中所给条件导致本题没思路。
正确答案
(Ⅱ)
解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
⑵直线AM的方程为
联立
解得

所以
所以
因为
所以

因为椭圆E的焦点在x轴,所以

解得


考查方向
解题思路
(2)设



易错点
不知如何运用题中所给条件导致本题没思路。
已知椭圆








22. 设






23. 设



正确答案
(1)略.
解析
试题分析:(1)依题意,直线l1的方程为
(1)证明:直线




所以
考查方向
解题思路
涉及弦长问题利用弦长公式解决,往往会更简单..
易错点
直线与椭圆的位置关系的计算问题
正确答案
(1)略(2)
解析
试题分析:(2)设直线l1的斜率为k,则直线l2的斜率为

(2)解:设



由

同理
由(1),
整理得
考查方向
解题思路
解决直线与椭圆的位置关系的相关问题,其常规思路是先把直线方程与椭圆方程联立,消元、化简,然后应用根与系数的关系建立方程,解决相关问题.
易错点
三角形面积公式的选用
已知椭圆




24. 求直线FM的斜率;
25. 求椭圆的方程;
26. 设动点P在椭圆上,若直线FP的斜率大于
正确答案
(I) 
解析
(I) 由已知有



设直线





考查方向
解题思路
(I) 由椭圆知识先求出



易错点
粗心出错。
正确答案
(II) 
解析
(II)由(I)得椭圆方程为











考查方向
解题思路
(II)由(I)设椭圆方程为



易错点
不会转化。
正确答案
(III) 
解析
(III)设点











设直线




①当



②当



综上,直线
考查方向
解题思路
(III)设出直线




易错点
不会进行分类。
10.如图,在平面直角坐标系





正确答案

解析
由题意得



由



则



考查方向
解题思路
设出各点坐标,根据向量数量积,列出方程,得到关于a,c的方程,求出e。
易错点
设点求解时正确建立方程关系。
知识点
设椭圆






24.求椭圆的方程;
25.设过点












正确答案
(Ⅰ)
解析
本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
(1)解:设







考查方向
解题思路
(Ⅰ)求椭圆标准方程,只需确定量,由



易错点
第二问不知如何处理已知条件导致本题没思路。
正确答案
(Ⅱ)
解析
本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
(2)由已知,设

设



由韦达定理

令
∵
即
∴
∴

所以,直线

考查方向
解题思路
(Ⅱ)先化简条件:
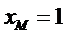


易错点
第二问不知如何处理已知条件导致本题没思路。
已知椭圆








26.求椭圆



27.设










正确答案
(Ⅰ)

解析
试题分析:(I)根据椭圆的几何性质得出得到椭圆中长半轴,短半轴,半焦距之间的关系求解即可.
(Ⅰ)由于椭圆












考查方向
解题思路
本题考查双曲线的几何性质,重点考查双曲线的渐近线方程,本题属于基础题,正确利用双曲线的标准方程,求出渐近线方程,求渐近线方程的简单方法就是把标准方程中的“1”改“0”,利用已知渐近线方程,求出参数
易错点
椭圆的几何性质
正确答案
(Ⅱ)存在点
解析
试题分析:(II)求解得出M,N点坐标,运用图形得出
(Ⅱ)







则







考查方向
解题思路
根据直线与椭圆的位置关系,设出点M,N坐标,然后根据几何关系结合坐标运算求得点Q的坐标即可证明问题.
易错点
角相等于斜率的关系
已知椭圆E:


20.求椭圆E的方程;
21.设直线

正确答案
(Ⅰ)
解析
(Ⅰ)由已知得

所以椭圆E的方程为
考查方向
解题思路
根据题意找到等量关系,建立关于参数的三元方程组,求得a b c的值
易错点
椭圆的性质掌握不好,计算能力弱
正确答案
(Ⅱ) G
解析
(Ⅱ)设点

由
所以

所以

故
所以

考查方向
解题思路
根据条件设出参数,然后根据参数间的等量关系建立方程,求解方程,进而达到参数的值,然后判断点和圆的位置关系。
易错点
计算能力弱,直线和圆锥曲线的综合求解能力弱
已知椭圆








24. 设






25. 设



26. 设






正确答案
(1)略
解析
试题分析:(1)依题意,直线l1的方程
(1)直线

由点到直线的距离公式得点


因为
所以
考查方向
解题思路
直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查,一直是高考考查的重点,特别是焦点弦和中点弦等问题,涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法,也是考查数学思想方法的热点题型.
易错点
准确计算化简
正确答案
((2)

解析
试题分析:(2)由(1)得:
(2)由


由(1)得
由题意知
解得

考查方向
解题思路
直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查,一直是高考考查的重点,特别是焦点弦和中点弦等问题,涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法,也是考查数学思想方法的热点题型.
易错点
面积公式的恰当选取运用
正确答案
(3)
解析
试题分析:(3)设直线l1的斜率为k,则直线l1的方程为y=kx,联立方程组







得到
(3)设



由

同理
由(1)知,

整理得
由题意知

则

所以
考查方向
解题思路
直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查,一直是高考考查的重点,特别是焦点弦和中点弦等问题,涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法,也是考查数学思想方法的热点题型.当直线(斜率为k)与圆锥曲线交于点A(x1,y1),B(x2,y2)时,则|AB|=


易错点
化简计算及方程恒成立问题
设椭圆






23.求E的离心率e;
24.设点C的坐标为

正确答案
(I)
解析
(Ⅰ)由题设条件知,点





考查方向
解题思路
(Ⅰ)由题设条件,可得点





易错点
椭圆方程相关性质、概念、公式记忆错误,计算能力弱
正确答案
解析
(Ⅱ)由题设条件和(Ⅰ)的计算结果可得,直线


















考查方向
1.椭圆的离心率;2.椭圆的标准方程;3.点点关于直线对称的应用.
解题思路
由题设条件和(Ⅰ)的计算结果知,直线

















易错点
圆锥曲线的相关性质、概念、公式记忆错误,计算能力弱
扫码查看完整答案与解析