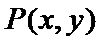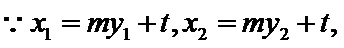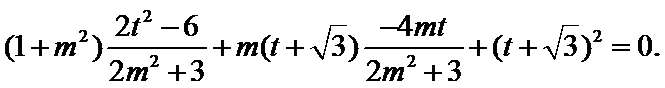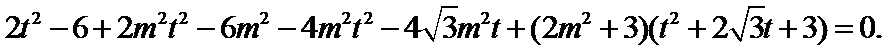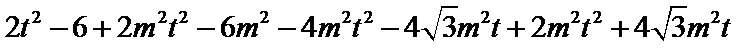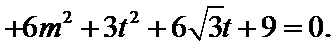- 椭圆及其性质
- 共751题
已知椭圆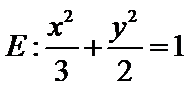
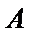
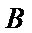
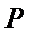
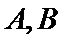
24.求直线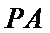
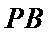

25.设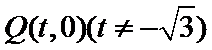

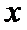

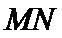
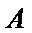

正确答案
直线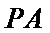
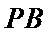
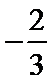
解析
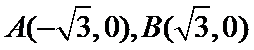
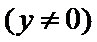
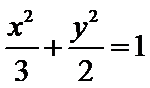
考查方向
解题思路
解题步骤如下:由椭圆的方程,可得到A ,B两点的坐标,设出点P(x,y),即可表示出直线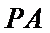
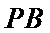
易错点
本题是综合性比较强的大题,涉及到的的知识点比较多,计算量较大,所以在计算时易发生错误 。
正确答案
存在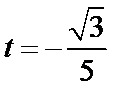
解析
【解析】令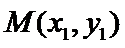
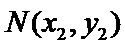
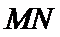
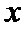
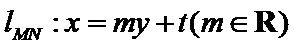
由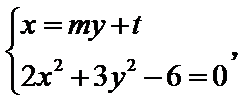
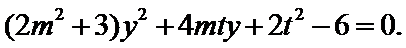
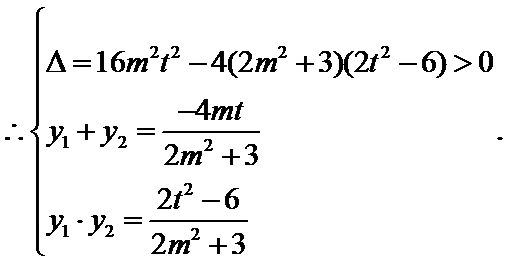
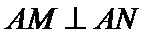
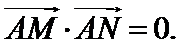
将(*)式代入上式,得
即
展开,得
整理,得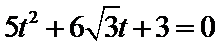
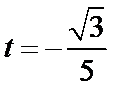
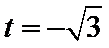
经检验,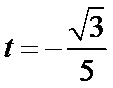
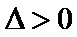
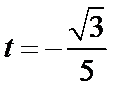
考查方向
解题思路
解题步骤如下:要满足以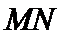
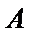

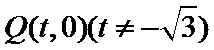
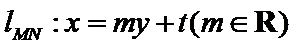
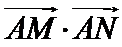
易错点
本题是综合性比较强的大题,涉及到的的知识点比较多,计算量较大,所以在计算时易发生错误 。
已知椭圆

25.求以线段
26.过点







正确答案

解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时利用椭圆定义完成第一问。再由“

(I)因为


所以以线段

考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:根据题意直接写出以线段


易错点
本题第二问在“

正确答案

解析
试题分析:本题是直线与圆锥曲线综合应用问题,解题时利用椭圆定义完成第一问。再由“

则直线



等价于
依题意,直线


由

因为直线


即

设





令

当

所以
化简得,
所以
当
所以存在点

考查方向
解题思路
本题考查直线与圆锥曲线综合应用问题,解题步骤如下:根据题意直接写出以线段


易错点
本题第二问在“

已知椭圆

22.求椭圆E的方程;
23.设经过

正确答案
(1)
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)待定系数法解;(2)用设而不求的方法来解答。
(I)设椭圆E:
考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)待定系数法解;(2)用设而不求的方法来解答。
易错点
计算量大,计算不出来。
正确答案
(2)x=4
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)待定系数法解;(2)用设而不求的方法来解答。
(II)将直线



直线AM的方程为

直线BN的方程为

联立得
或

考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)待定系数法解;(2)用设而不求的方法来解答。
易错点
计算量大,计算不出来。
已知椭圆


21.求椭圆
22.从椭圆








正确答案
(1)
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)根据已经条件构造方程组;(2)先将
(1)


……4分
考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)根据已经条件构造方程组;(2)先将
易错点
计算不出来。
正确答案
(2)
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)根据已经条件构造方程组;(2)先将
(2)设点














所以

考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)根据已经条件构造方程组;(2)先将
易错点
计算不出来。
11.已知直线







正确答案
知识点
20.已知椭圆


(1)求实数m的
(2)求△AOB面积的最大值(O为坐标原点).
正确答案
(1)


解析
试题分析:(1)可设直线AB的方程为y=



(1)由题意可知m











(2)令



∴S(t)=




考查方向
解题思路
(1)设出直线AB的方程,把椭圆和直线方程联立,利用中点的坐标公式,根
与系数的关系求解;(2)表示出三角形的面积,利用二次函数求出最大值即可.
易错点
计算要细心.
知识点
为达到某一专门目的或解决某一专门问题而对员工进行的培训是( )。
A.项目培训
B.操作层员工的知识和能力培训
C.专题培训
D.管理层员工的知识和能力培训
正确答案
C
解析
暂无解析
已知椭圆













22.求椭圆
23.当




正确答案
详见解析
解析
解:依题意


又


考查方向
椭圆的标准方程
解题思路
设出参数,根据等量关系建立方程,求解参数,进而求出椭圆的方程
易错点
计算错误,相关定理公式掌握不牢固
正确答案
详见解析
解析
由1)知圆

圆心O到直线
















…………13分
考查方向
椭圆的性质及应用,直线与圆锥曲线的综合题
解题思路
利用点到直线的距离公式,建立等量关系,然后利用这个关系求解可得
易错点
计算能力弱
市场营销组合的特点有( )
A.对企业来说都是“不可控因素”
B.是一个单一结构
C.是一个静态组合
D.要受企业市场定位战略的制约
正确答案
D
解析
暂无解析
如图,在平面直角坐标系xoy中,椭圆

26.求椭圆的方程;
27.若直线AB斜率为1时,求弦AB长;
28.过椭圆的对称中心O,作直线L,交椭圆与M,N,三角形FMN是否存在在大面积?若存在,求出它的最大面积值。若不存在,说明理由
正确答案
当AB的斜率为0时,AB=半长轴,即
2a=4,a=2;
又因为 e=c/a,
又
所以解析式为
解析
看解题步骤
考查方向
圆锥曲线
解题思路
利用离心率公式。abc之间的关系
易错点

教师点评
考查圆锥曲线解析式求解
正确答案
联立直线与椭圆方程得:5x2-8x=0设方程根为x1=0,x2=8/5,
|AB|=
解析
见答案
考查方向
直线与圆锥曲线的关系,两点之间的距离
解题思路
先求出两焦点的横坐标,利用距离与斜率、求两点间的距离公式求解
易错点
无
教师点评
考查了直线与圆锥曲线的关系,和用斜率求两点距离
正确答案
S⊿FMN= 

扫码查看完整答案与解析