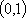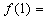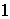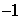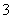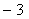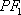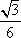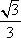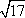- 椭圆及其性质
- 共751题
设
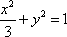
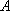
正确答案
解析
设直线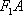
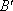
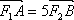
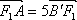
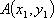
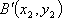
又∵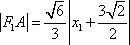
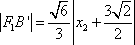
∴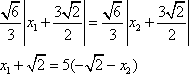
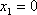
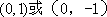
知识点
已知椭圆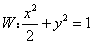
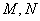
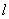
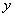
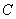
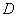
(1)若直线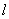
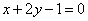
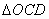
(2)判断是否存在直线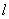
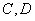
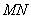
正确答案
见解析
解析
(1)证明:因为直线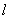
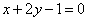
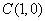
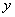
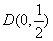
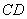
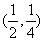
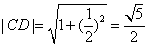
即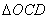
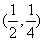
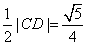
所以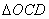
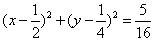
(2)解:结论:存在直线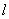
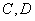
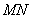
由题意,设直线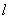
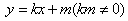
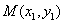
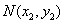
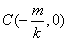
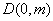
由方程组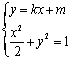
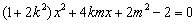
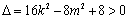
由韦达定理,得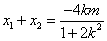
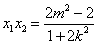
由
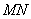
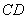
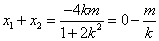
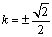
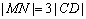
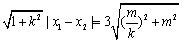
即 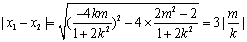
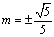
所以存在直线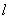
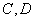
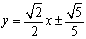
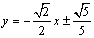
知识点
已知函数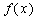
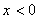
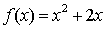
正确答案
解析
略
知识点
已知




正确答案
2
解析
略
知识点
如图,非零向量




取值范围是 。
正确答案
解析
略
知识点
设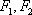
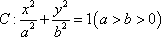
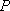
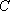
的中点在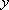
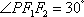
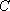
正确答案
解析
略
知识点
设






正确答案
解析
略
知识点
如图,







正确答案
解析
由已知得



知识点
已知圆锥底面半径与球的半径都是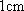
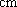
正确答案
解析
略
知识点
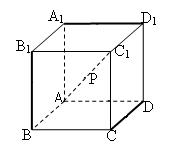
在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD 、A1D1、 BB1的距离都相等,则这样的点共有
正确答案
解析
略
知识点
扫码查看完整答案与解析