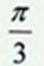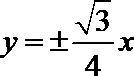- 椭圆及其性质
- 共751题
已知椭圆








正确答案
解析
过点B作





知识点
如图,设椭圆中心在坐标原点,




(1)若

(2)求四边形
正确答案
见解析
解析
(1)依题可设得椭圆的方程为
直线
设



由
点

所以

(2)解法1:根据点到直线的距离公式和①式知,点

又

当



解法2:由题设,
设






知识点
已知椭圆C:


(1)求椭圆C的方程;
(2)记椭圆C的上顶点为B,直线l交椭圆C于P,Q两点,问:是否存在直线l,使椭圆C的右焦点F2恰为△PQB的垂心(△PQB三条边上的高线的交点)?若存在,求出直线l的方程,若不存在,请说明理由。
(3)若⊙M是以AF2为直径的圆,求证:⊙M与以坐标原点为圆心,a为半径的圆相内切。
正确答案
见解析。
解析
(1)∵椭圆C:

∴
该椭圆上一点A与左、右焦点F1,F2构成的三角形周长为2
∴|AF1|+|AF2|+|F1F2|=2a+2c=
解得a=

∴椭圆C的方程为
(2)假设存在直线l,使椭圆C的右焦点F2恰为△PQB的垂心。
设P(x1,y1),Q(x2,y2),则BF2⊥PQ。
∵B(0,1),F2(1,0),∴
设直线l的方程为:y=x+m,联立
化为3x2+4mx+2m2﹣2=0,则x1+x2=

∵
∴x1(x2﹣1)+y2(y1﹣1)=0,
∴x1(x2﹣1)+(x2+m)(x1+m﹣1)=0,化为2x1x2+(x1+x2)(m﹣1)+m2﹣m=0,
∴


经检验m=﹣

(3)证明:设A(x0,y0),F2(1,0),则M
设两圆的半径分别为r1,r2。
|OM|=


又⊙M的半径r1=|MF2|=

∴r2﹣r1=

∴|OM|=r2﹣r1。
∴⊙M与以坐标原点为圆心,a为半径的圆相内切。
知识点
离心率为



正确答案
解析
解析:
设椭圆



















知识点
15.如图,椭圆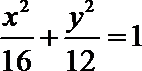
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若椭圆经过点P(2,3),且焦点为F1(-2,0),F2(2,0),则这个椭圆的离心率等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知椭圆
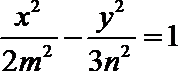
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知定直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆




(1)(ⅰ)若圆

(ⅱ)若椭圆上存在点


(2)设直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析