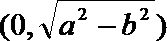- 椭圆及其性质
- 共751题
14.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
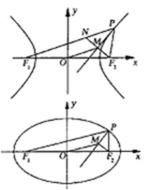
16.如图,P是双曲线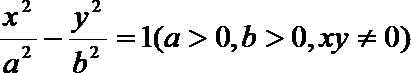
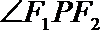
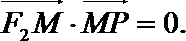
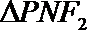
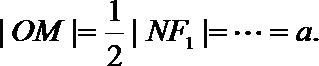
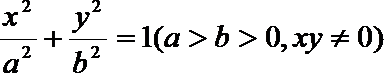
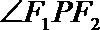
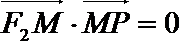
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知点P是椭圆


正确答案
解析
如图,
当点P在椭圆与y轴交点处时,点M与原点O重合,
此时|
当点P在椭圆与x轴交点处时,点M与焦点F1重合,
此时|

∵xy≠0,∴|

知识点
20. 如图,已知椭圆





(Ⅰ)设直线




(Ⅱ)是否存在常数


正确答案
(Ⅰ)设

因为点P在双曲线

因此

(Ⅱ)由于PF1的方程为

得
所以
同理可得

又
故
因此,存在

解析
解析已在路上飞奔,马上就到!
知识点
8. 已知直线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.将曲线 

正确答案
(±
解析
解析已在路上飞奔,马上就到!
知识点
21.已知直线


(1)若椭圆的离心率为
(2)若向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知双曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知椭圆
正确答案
解析
知识点
扫码查看完整答案与解析