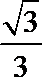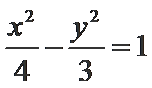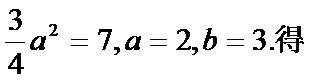- 双曲线的几何性质
- 共220题
12．若点P在曲线C1：
正确答案
10
解析
解析已在路上飞奔，马上就到！
知识点
2.如果双曲线的渐近线方程为
A
B
C
D
正确答案
解析
由渐近线方程为
得
那么
或
知识点
13.如果圆锥曲线
正确答案
解析
若
则有(λ+5)(2-λ)>0,
即-5<λ<2,
这时a2=λ+5,b2=2-λ,
于是
得此时的焦点坐标为
若
则有
这时a2=λ+5,b2=λ-2,
于是
显然焦点在y轴上,
得此时的焦点坐标为
知识点
2.如果双曲线的渐近线方程为
A
B
C
D
正确答案
解析
由渐近线方程为
得
那么
或
知识点
4.过双曲线
正确答案
解析
当|AB|=2时,只有一条,此时是x轴;
当|AB|=4时,有三条,其中两条交在两支上,另一条垂直于x轴.
那么当2<|AB|<4时,有两条.
知识点
4.过双曲线
正确答案
解析
当|AB|=2时,只有一条,此时是x轴;
当|AB|=4时,有三条,其中两条交在两支上,另一条垂直于x轴.
那么当2<|AB|<4时,有两条.
知识点
13．已知抛物线
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．过双曲线
A
B
C3
D
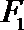
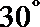
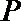
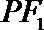
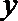
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
30．如图，点
正确答案
解析
试题分析：本题属于圆锥曲线中的偏难问题，题目的难度较大，
（1）直接按照步骤来求
（2）要注意对参数的讨论．
存在一条双曲线，对任意的正整数
如图所示，
所以
当
所以
当且仅当
故
考查方向
本题考查了直线与圆锥曲线的位置关系，属于高考中的高频考点．
解题思路
本题考查圆锥曲线与直线的位置关系，表示出直线斜率依次求解。
易错点
表示直线斜率时容易出错。
知识点
10．已知双曲线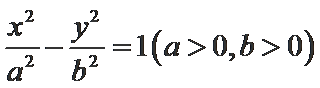
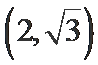
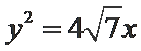
正确答案
解析
将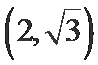
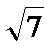
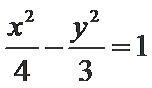
考查方向
解题思路
本题考查运用双曲线的渐近线方程及抛物线的准线方程，求a,b，解题步骤如下：将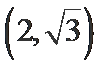
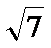
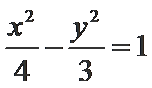
易错点
本题必须注意审题，忽视则会出现错误。
知识点
扫码查看完整答案与解析