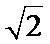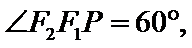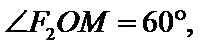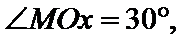- 双曲线的几何性质
- 共220题
1.若双曲线
正确答案
解析
本题属于双曲线中的基本问题,题目的难度是简单。
考查方向
主要考查了双曲线的标准方程,在近几年的各省高考题出现的频率较高。
解题思路
无
易错点
本题易在求解时把分母平方运算。
知识点
11.双曲线C:




正确答案
解析
由于MN∥F1F2,





考查方向
解题思路
确定N、Q的坐标,代入双曲线方程,即可求出双曲线的离心率。
易错点
本题容易因为对双曲线的性质记忆不清楚而导致题目无法进行。
知识点
11.双曲线C:




正确答案
解析
如下图所示,由












考查方向
解题思路
先分别求出两个集合中代表元素的取值范围,再求交集。
易错点
对于已知条件
知识点
9.已知点











正确答案
解析
由题意得:





知识点
11. 已知双曲线




正确答案
解析
利用交点这一突破口,建立方程关系,进而求出a和c的关系,所以得到离心率为
考查方向
解题思路
先设交点坐标,与渐近线联立方程组,最后用余弦定理求得
易错点
计算错误、离心率、渐近线方程错误
知识点
8. 设F1、F2是双曲线
△PF1F2的面积是( )
正确答案
解析
设其中较小的直角边长为






考查方向
解题思路
根据双曲线定义,设其中较小的直角边长为



易错点
忘记双曲线的定义,不记得两个焦半径之间的边长关系,导致无法列方程求出边长,也就无法求出面积。
知识点
11.过点






正确答案
解析
过点


解得
考查方向
解题思路
因为双曲线是无限接近于它的渐近线的,所以双曲线到直线的距离恒大于
易错点
不能将曲线到直线的距离转化成直线到直线的距离,导致计算繁琐甚至出错
知识点
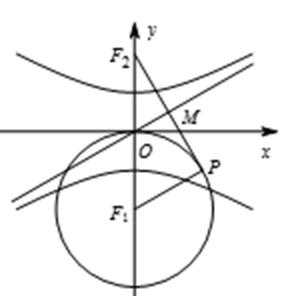
11.如图,已知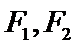
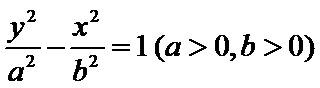
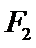
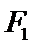
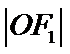
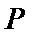
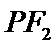
正确答案
解析
设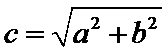
由题意得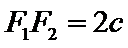
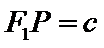
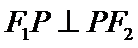
所以
因为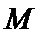
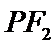
所以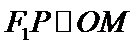
所以
所以
而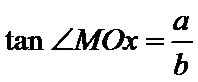
所以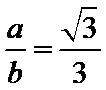
所以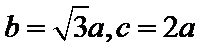
所以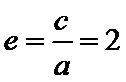
考查方向
解题思路
1、选根据题中条件求出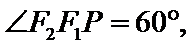
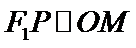
2.利用渐近线的斜率得到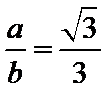
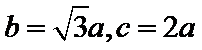
易错点
1、无法将题中条件准确转化;
2.焦点在y轴上的双曲线的渐近线的方程与焦点在x轴上的渐近线方程不同,此点容易出错。
知识点
11.F为双曲线


正确答案
解析
若设双曲线的左焦点为F’,
连接P F’,
由几何关系可知三角形P F’F是直角三角形,
PF’=
所以PF’-PF=
所以e=
故选D。
考查方向
解题思路
若设双曲线的左焦点为F’, 连接P F’,由几何关系可知三角形P F’F是直角三角形,然后利用双曲线的定义即的a与c的关系,从而求得离心率。
易错点
若设双曲线的左焦点为F’,不能想到连接P F’,利用双曲线的定义解题。
知识点
9.






正确答案
解析
直线PF的方程为y=x-2,与抛物线方程联立,解得x=4,所以
考查方向
解题思路
本题考查抛物线的简单几何性质,解题步骤如下:1、由题可知,易得直线PF的方程。2、将直线方程与抛物线联立,解得
易错点
本题易在求解时把分母平方运算。
知识点
扫码查看完整答案与解析