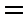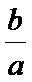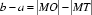- 双曲线的几何性质
- 共220题
15.在平面直角坐标系
正确答案
解析
.
根据题意写出渐近线方程
所以
所以
考查方向
解题思路
该题思路比较清晰，主要有以下几个步骤1、求双曲线的渐近线2、根据圆的性质求出圆的方程3、渐近线与椭圆联立求出AB点坐标4、利用圆心到A的距离等于半径求出关系式
易错点
本题易错点主要集中在，1、渐近线的表达，2、外接圆的几何性质
知识点
抛物线
正确答案
解析
根据抛物线
考查方向
本题主要考查了抛物线准线的定义与双曲线的渐近线的定义的综合应用
易错点
容易记错抛物线准线的定义
知识点
7．设双曲线
同，则此双曲线的方程为
A
B
C
D
正确答案
解析
由c=1,且焦点在y轴上,得a=2b。A选项不正确，B选项不正确，C选项不正确，所以选D选项。
考查方向
本题主要考查双曲线的标准方程
解题思路
1、求出c；
2、利用a,b,c关系求a,b，即可得到结果。A选项不正确，B选项不正确，C选项不正确，所以选D选项。
易错点
本题易在判断焦点位置时发生错误。
知识点
3．若实数数列：
A
B
C
D
正确答案
解析
由a22=81得a2=9，则
考查方向
本题主要考查数列、椭圆的离心率运算
解题思路
1、求出a2；
2、求出e，即可得到结果。
A选项不正确，B选项不正确，D选项不正确，所以选C选项。
易错点
本题易在求a2时发生错误。
知识点
6.已知点
A
B
C
D
正确答案
解析
根据题意作图
容易得到
由双曲线的几何性质
考查方向
解题思路
【解题思路】本题属于基础题型，使用数形结合，
易错点
该题不易发现使用几何性质，导致运算变大，运算出错
知识点
10.设双曲线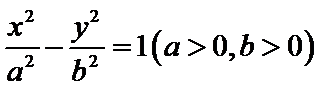
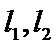
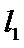
A3
B2
C
D
正确答案
解析
过F和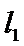
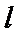
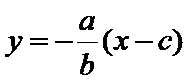
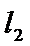
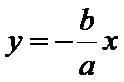
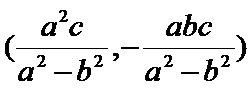
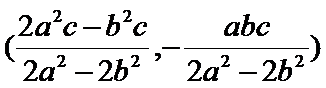
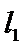
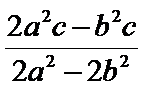
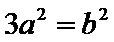
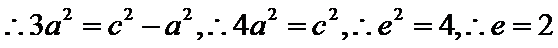
知识点
9．已知双曲线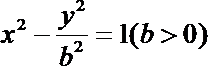
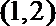
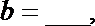
正确答案
2;
解析
双曲线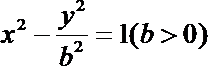
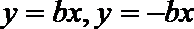
易错点
本题易在记忆双曲线的渐近线方程时发生错误从而导致b值的错误。
知识点
10．已知椭圆
A1
B
C
D2
正确答案
解析
设椭圆的点为
考查方向
本题主要考查了圆锥曲线的切线方程、面积计算和函数的最值问题,属于难度较大的题，常考求方程、离心率的值或范围、中点弦，面积等问题。
易错点
本题难在方程的合理假设与面积的计算易在集合的交并补运算上出问题。
知识点
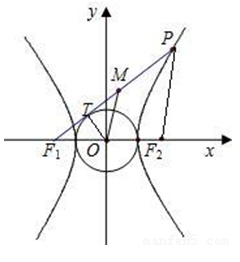
11．过双曲线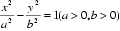
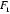
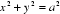
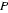
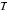
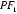
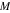
A
B
C
D
正确答案
解析
解：连OT，则OT⊥F1T，在直角三角形OTF1中，|F1T|=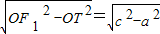
连PF2，M为线段F1P的中点，
O为坐标原点∴OM=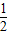
∴|MO|-|MT|=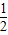
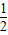
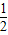
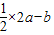
点评：本题主要考查双曲线的定义及三角形中位线和直线与圆相切时应用勾股定理．解答的关键是熟悉双曲线的定义的应用，直线与圆的位置关系以及三角形中的有关结论。B选项不正确，C选项不正确，D选项不正确，所以选A选项。
考查方向
本题主要考查双曲线与圆的知识
易错点
本题易在利用双曲线定义时发生错误。
知识点
7.已知双曲线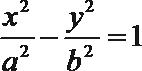
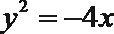
A
B
C
D
正确答案
解析
双曲线的左焦点为(-2,0),即c=2，所以a=1,b2=3,所以选D
考查方向
本题主要考查双曲线与抛物线的几何性质,属于简单题
解题思路
先求出a,b的值,进而求解问题
易错点
双曲线的标准方程等基础概念
知识点
扫码查看完整答案与解析