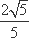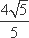- 双曲线的几何性质
- 共220题
1
题型:
单选题
|
双曲线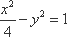
正确答案
C
解析
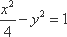
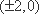
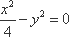
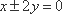
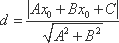
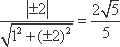
知识点
双曲线的几何性质
1
题型:
单选题
|
已知双曲线

正确答案
C
解析
设A点坐标为(x0,y0),则由题意,得S△AOB=|x0|·|y0|=








知识点
双曲线的几何性质抛物线的标准方程和几何性质
1
题型:填空题
|
设直线





正确答案
解析
由双曲线的方程可知,它的渐近线方程为





设AB中点为

即
∴




知识点
双曲线的几何性质
1
题型:简答题
|
设函数

(1) 当

(2) 当



正确答案
(1) 

解析
(1) 当

令

当

右表可知,函数



(2)
令


令



所以

所以当



所以
令

令
所以

所以存在



当

所以


因为

所以



综上,函数


知识点
双曲线的几何性质
1
题型:
单选题
|
如图,







正确答案
D
解析
由已知得



知识点
椭圆的几何性质双曲线的几何性质直线、圆及圆锥曲线的交汇问题
已完结
扫码查看完整答案与解析