热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设F1，F2分别为双曲线的左、右焦点。若在双曲线右支上存在点P，满足，且F2到直线PF1的距离等于双曲线的实轴长，则该双曲的渐近线方程为

正确答案

解析

本题考查了双曲线的定义、解三角形

易知PF2＝4b，则4b－2c＝2a，又c2＝a2＋b2，得3b＝4a，故渐近线方程为4x±3y＝0

知识点

双曲线的几何性质

题型：填空题

填空题 · 4 分

已知当时，函数的最小值为-4，则t的取值范围是

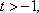
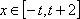
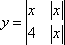
正确答案

解析

略

知识点

双曲线的几何性质

题型：单选题

单选题 · 5 分

如图，F1，F2分别是双曲线C：(a，b＞0)的左右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M，若|MF2|＝|F1F2|，则C的离心率是

正确答案

解析

如图：|OB|＝b，|O F1|＝c，∴kPQ＝，kMN＝﹣。

直线PQ为：y＝(x＋c)，两条渐近线为：y＝x，由，得：Q(，)；由，得：P(，)，∴直线MN为：y－＝﹣(x－)，

令y＝0得：xM＝，又∵|MF2|＝|F1F2|＝2c，∴3c＝xM＝，解之得：，即e＝。

知识点

双曲线的几何性质直线、圆及圆锥曲线的交汇问题

题型：填空题

填空题 · 4 分

已知全集，则=

正确答案

解析

略

知识点

双曲线的几何性质

题型：单选题

单选题 · 5 分

7．已知双曲线的左、右焦点分别为F1、F2，P为双曲线C的右支上一点，且|PF2|＝|F1F2|，则ΔPF1F2的面积等于（）

A24

B36

C48

D96

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的几何性质

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 双曲线的几何性质

扫码查看完整答案与解析