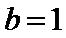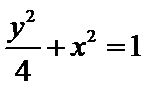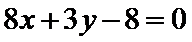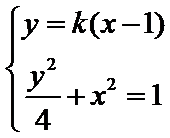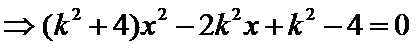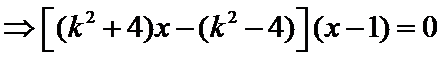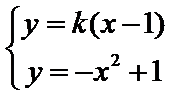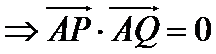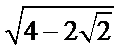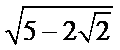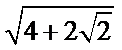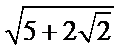- 双曲线的几何性质
- 共220题
12.已知抛物线






正确答案
解析
抛物线









则
因为


考查方向
解题思路
1.先根据抛物线的焦点求出双曲线的方程;
2.设出P点到坐标后表示函数
易错点
1.抛物线的焦点求错导致双曲线的方程出错;
2.不会构造函数求解
知识点
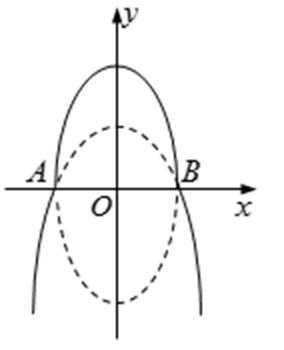
如图,曲线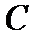
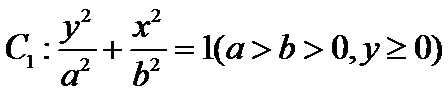
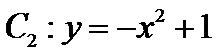
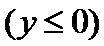
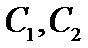
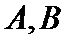
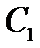
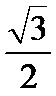
23.求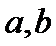
24.过点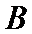

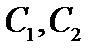
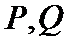
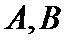
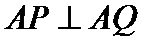

正确答案
(1)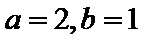
解析
(Ⅰ)因为抛物线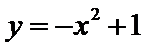
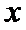
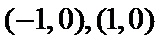
由因为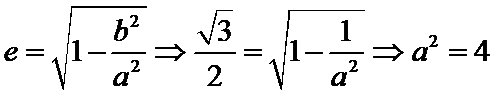
考查方向
解题思路
先根据抛物线与x轴的交点求出b的值,后利用离心率求出a的值;
易错点
不知道抛物线与x轴的交点即为b的值;
正确答案
(2)
解析
(Ⅱ)因为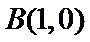
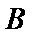
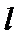
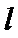
设直线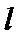
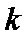
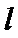
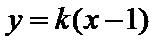
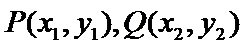
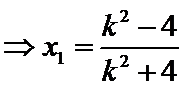
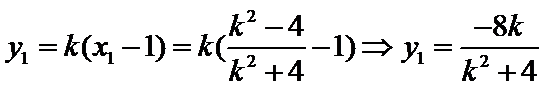
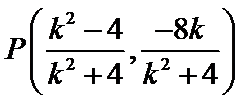
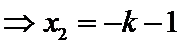
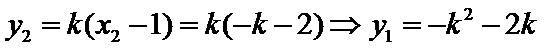
由
化简得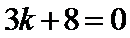
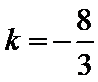
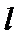
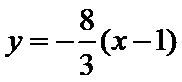
考查方向
解题思路
设出直线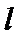
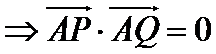
易错点
不会转化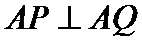
9.双曲线
正确答案


解析
试题分析:由双曲线

∵双曲线




考查方向
解题思路
根据双曲线的方程求出2c和渐近线方程。
易错点
注意双曲线中焦距为2c,双曲线的渐近线方程。
知识点
5.过双曲线

正确答案
解析
双曲线的右焦点为




考查方向
解题思路
先根据双曲线方程求出基本量后,将


易错点
将双曲线中的基本量与椭圆中的混淆导致出错;将
知识点
9. 等腰直角三角形ABC中,A=90°,A,B在双曲线E的同一支上,且线段AB通过双曲线的一个焦点,C为双曲线E的另一个焦点,则该双曲线的离心率为
正确答案
解析
设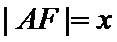
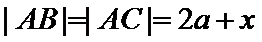
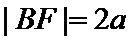
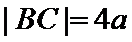
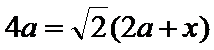
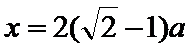
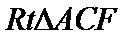
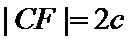
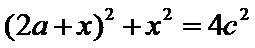
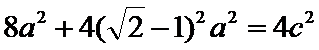

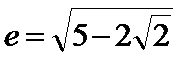
考查方向
解题思路
1)利用等腰三角形和双曲线的定义得到相关边的长度;
2)利用勾股定理和离心率公式进行求解.
易错点
本题易在选择双曲线的定义出现错误,易忽视双曲线的定义的灵活运用.
知识点
6.经过点(2,1),且渐近线与圆
正确答案
解析
设渐近线方程为
∴渐近线为
∴设双曲线方程为
考查方向
解题思路
1)设渐近线方程
2)利用渐近线写出含参双曲线方程,带入坐标直接得出结果
易错点
本题易在双曲线焦点的判断
知识点
14. 已知双曲线





正确答案
解析
设双曲线的离心率为e,

考查方向
解题思路
先由题意及双曲线的定义,可得

易错点
利用焦半径公式易出错,寻找a,b,c关系时找不到突破口
知识点
3.若双曲线的顶点和焦点分别为椭圆
正确答案
解析
由椭圆方程





因此B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
根据已知椭圆方程写出其焦点和顶点坐标,从而知双曲线的顶点和焦点坐标,由此确定a,b,c的值最后给出双曲线的方程。因此B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
易混淆椭圆与双曲线中a,b,c之间的关系以及a,b,c在两种曲线中所表示的意义。
知识点
6.过双曲线

正确答案
解析
由题意,得




考查方向
解题思路
根据题意求出A,B两点的坐标,由△OAB的面积为
故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
对△OAB的面积的转化较繁琐而出错。
知识点
10.双曲线

正确答案
解析
由题意可知,双曲线的一个渐近线方程为:



考查方向
解题思路
先求出渐近线方程,代入抛物线方程,从而推出a和c的关系。
易错点
计算能力差
知识点
扫码查看完整答案与解析