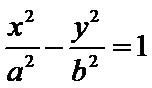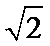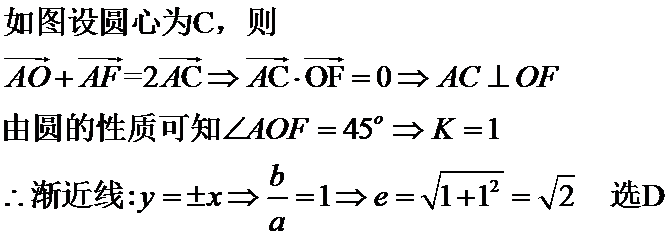• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 双曲线的几何性质
  • 共220题
  • 双曲线的几何性质
  • 共220题

热门试卷

X 查看更多试卷
1
题型：填空题
|
填空题 · 5 分

15.已知分别为双曲线的两条渐近线，且右焦点关于的对称点在上，则双曲线的离心率为        .

正确答案

2

解析

由题意得的方程分别为，右焦点的坐标为（c,0）,设右焦点关于的对称点的坐标为（m,n）,则，解得，又（m,n）在上，所以，化简得，所以，得离心率为2.

考查方向

本题主要考查双曲线的几何性质等知识，意在考查考生的数形结合能力和运算求解能力。

解题思路

1.先根据题意先表示出的方程分别为，右焦点的坐标为（c,0），设出对称点的坐标为（m,n）求出；2.将点（m,n）带入得到a,b之间的关系即可求出离心率。

易错点

1.点（m,n）的坐标求错；2.不会建立关于a,b,c之间的关系。

知识点

双曲线的定义及标准方程双曲线的几何性质直线、圆及圆锥曲线的交汇问题
1
题型： 单选题
|
单选题 · 5 分

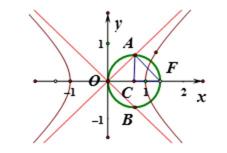
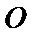
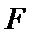
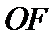
6.已知为坐标原点，双曲线的右焦点为，以为直径作

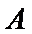
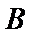
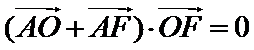
圆交双曲线的渐近线于两点，（异于原点），若，则双曲线的离

心率为（）

A

B

C

D

正确答案

D

解析

由题意作图

考查方向

本题考察了双曲线的几何性质，考察了圆的几何性质，考察了向量的平行四边形法则，考察了数量积运算，属于中档题

解题思路

1、根据题意画出简图

2、找到向量的性质直接得出a，b的关系

易错点

主要易错于圆的性质的判断，以及向量的几何意义的判断

知识点

双曲线的定义及标准方程双曲线的几何性质直线、圆及圆锥曲线的交汇问题
1
题型： 单选题
|
单选题 · 5 分

6.过双曲线的一个焦点作双曲线的一条渐近线的垂线，若垂线的延长线与轴的交点坐标为，则此双曲线的离心率是（）

A

B

C

D

正确答案

D

解析

设,由题意得到MF垂直于渐近线，所以，化简得，所以，离心率为，故选D。

考查方向

本题主要考查圆锥曲线的性质，两条直线的位置关系等知识，意在考查考生数形结合的能力和转化与化归的能力。

解题思路

1.根据直线间的垂直关系求出，进而求出；2.带入离心率的公式求解即可。

易错点

1.不会转化过双曲线的一个焦点作双曲线的一条渐近线的垂线这个条件；2，图形语言的转化有障碍。

知识点

双曲线的定义及标准方程双曲线的几何性质直线、圆及圆锥曲线的交汇问题
1
题型： 单选题
|
单选题 · 5 分

4.设双曲线上的点P到点的距离为6，则P点到的距离是（   ）

A2或10

B10

C2

D4或8

正确答案

A

解析

双曲线a=2,b=1,c=,它的左右焦点分别是，，由定义有所以 ，。选A

考查方向

本题主要考查双曲线的定义和几何性质等知识，意在考查考生的运算求解能力和转化的能力。

解题思路

1.根据双曲线方程求出双曲线的基本量a,b,c;2.利用双曲线的定义得到。

易错点

1。之间的关系和椭圆的混淆出错；2.不会转化为双曲线的定义解决问题。

知识点

双曲线的几何性质直线、圆及圆锥曲线的交汇问题
1
题型：填空题
|
填空题 · 5 分

已知双曲线C的离心率为2，左、右焦点为，点A在C上，若，则          。

正确答案

考查方向

本题主要考查了双曲线的定义和解三角形,属于中档难度的题，常考求方程、离心率的值或范围、中点弦，面积等问题。

解题思路

本题主要考查了双曲线的定义和解三角形，解题步骤如下：

易错点

本题易在运算上出问题。

知识点

双曲线的几何性质直线、圆及圆锥曲线的交汇问题
1
题型： 单选题
|
单选题 · 5 分

9．已知双曲线的左右焦点分别为，，若上存在点使为等腰三角形，且其顶角为，则的值是（   ）

A

B

C

D

正确答案

D

解析

因为是等腰三角形，且顶角为，，

由平面几何知识得，，根据双曲线的定义得，由双曲线的离心率得

，两边平方，得，故选D.

考查方向

本题主要考查了双曲线的几何性质、定义以及简单的平面几何知识，是圆锥曲线中很重要的考察对象，是高频考点。

解题思路

先画等腰三角形，利用平面几何知识以及双曲线的定义表示出离心率，即可解决问题。

易错点

不会画等腰三角形或不会用双曲线的定义解决问题。

知识点

双曲线的定义及标准方程双曲线的几何性质直线、圆及圆锥曲线的交汇问题
1
题型：简答题
|
简答题 · 16 分

已知抛物线，为抛物线上的点，若直线经过点且斜率为，则称直线为点的“特征直线”. 设、为方程（）的两个实根，记.

24.求点的“特征直线”的方程；

25.已知点在抛物线上，点的“特征直线”与双曲线经过二、四象限的渐进线垂直，且与轴的交于点，点为线段上的点. 求证：；

26.已知、是抛物线上异于原点的两个不同的点，点、的“特征直线”分别为、，直线、相交于点，且与轴分别交于点、. 求证：点在线段上的充要条件为（其中为点的横坐标）.

第(1)小题正确答案及相关解析

正确答案

（1）.；

解析

（1）由题意的斜率为1，

所以点的“特征直线”的方程为.

考查方向

本题主要考查圆锥曲线的的定义、性质、直线与圆锥曲线的位置关系、充要条件等知识，意在考查考生的理解能力，转化与划归的能力。

解题思路

1根据题意直接求出“特征直线”的方程为.

易错点

1.不理解特征直线的定义导致无法入手；2.证明充要条件时不知道应该证明充分性和必要性。

第(2)小题正确答案及相关解析

正确答案

（1）.；

解析

设点，由于双曲线所求渐进线的斜率为

所以，进而得

线段的方程为

所以满足

所对应方程为：，解得，

因为，所以，进而

考查方向

本题主要考查圆锥曲线的的定义、性质、直线与圆锥曲线的位置关系、充要条件等知识，意在考查考生的理解能力，转化与划归的能力。

解题思路

线根据渐近线方程求出，进而得到点（a,b）满足的方程；

易错点

1.不理解特征直线的定义导致无法入手；2.证明充要条件时不知道应该证明充分性和必要性。

第(3)小题正确答案及相关解析

正确答案

见解析

解析

(3)设，，则、的方程分别为

，，

解、交点可得，，

所对应的方程为：，

得

必要性：因为点在线段上，所以

当时，，得，

当时，，得，

所以，进而

① 充分性：由，得，

当时，，得，

当时，得，得，

所以点在线段上.

综上，点在线段上的充要条件为

考查方向

本题主要考查圆锥曲线的的定义、性质、直线与圆锥曲线的位置关系、充要条件等知识，意在考查考生的理解能力，转化与划归的能力。

解题思路

先证明结论的充分性，后证明其必要性。

易错点

1.不理解特征直线的定义导致无法入手；2.证明充要条件时不知道应该证明充分性和必要性。

1
题型： 单选题
|
单选题 · 5 分

10.双曲线（，）的左、右焦点分别是，过作倾斜角为 的直线交双曲线右支于点，若垂直于轴，则双曲线的离心率为（）

A

B

C

D

正确答案

C

解析

由题意知：，由直线的倾斜角为得即，所以解得舍），故选C。

考查方向

本题主要考查圆锥曲线的通径、离心率的求法等知识，意在考查考生的数形结合能力和运算求解能力。

解题思路

1.先根据题意求出M点到坐标；2.根据直线的倾斜角为得即，得到关于离心离的等式解方程即可。

易错点

1.不会求M点的坐标；

2.不会转化题中的倾斜角为45度。

知识点

双曲线的定义及标准方程双曲线的几何性质直线、圆及圆锥曲线的交汇问题
1
题型： 单选题
|
单选题 · 5 分

12．过点的直线与双曲线的一条斜率为正值的渐近线平行，若双曲线的右支上的点到直线的距离恒大于，则双曲线的离心率的取值范围是（   ）

A

B

C

D

正确答案

A

解析

根据题意，过(0.2b)与斜率为正的渐近线平行的直线方程为若双曲线的右支上的点到直线的距离恒大于，的距离大于等于2b即可，双曲线的离心率大于1，所以答案应选择A.

考查方向

本题考查直线与双曲线的位置关系问题。双曲线的离心率问题。

解题思路

借助双曲线和几何性质及直线与双曲线的关系，“双曲线的右支上的点到直线的距离恒大于”即两直线的距离与b的关系，得到重要不等式再结合双曲线中a,b,c的关系即可求解。

易错点

不能正确理解“双曲线的右支上的点到直线的距离恒大于”

知识点

双曲线的几何性质直线、圆及圆锥曲线的交汇问题
1
题型： 单选题
|
单选题 · 5 分

7.设双曲线C：的右焦点为，左、右顶点分别为，以为直径的圆与双曲线的一条渐近线交于点（点在第一象限内），若直线平行于另一条渐近线，则该双曲线离心率的值为

A

B

C

D3

正确答案

A

解析

如图，过P作PH垂直x轴，根据PF平行渐近线，所以三角形POF为等腰三角形，OH= ,OP=a, PH=在直角三角形OPH中，tan∠POH= ，化简整理得4,即4，所以e=

考查方向

考查双曲线的定义，渐近线，离心率

解题思路

画出双曲线的简图，结合双曲线渐近线的特点，得出a，b，c的数量关系，进而求出离心率

易错点

数形结合及数据推导容易出错

知识点

双曲线的几何性质直线、圆及圆锥曲线的交汇问题
继续学习 棒棒哒，已是最后一个知识点
已完结
百度题库 > 高考 > 理科数学 > 双曲线的几何性质

扫码查看完整答案与解析

  • 上一题
  • 1/10
  • 下一题