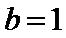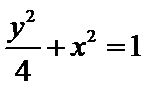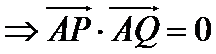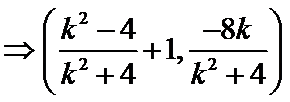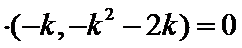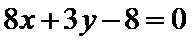- 双曲线的几何性质
- 共220题
12.已知抛物线






正确答案
解析
抛物线









则
因为


考查方向
解题思路
1.先根据抛物线的焦点求出双曲线的方程;
2.设出P点到坐标后表示函数
易错点
1.抛物线的焦点求错导致双曲线的方程出错;
2.不会构造函数求解
知识点
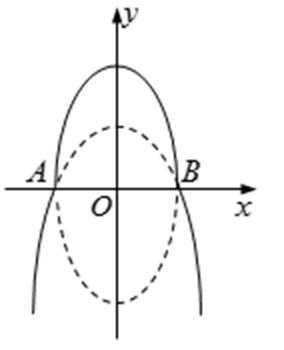
如图,曲线
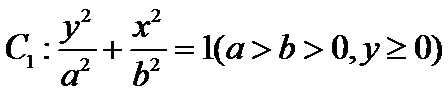
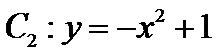
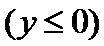
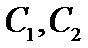
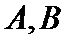
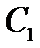
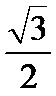
23.求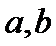
24.过点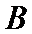

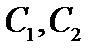
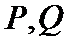
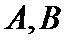
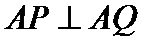

正确答案
(1)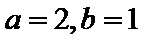
解析
(Ⅰ)因为抛物线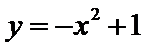
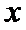
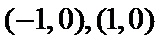
由因为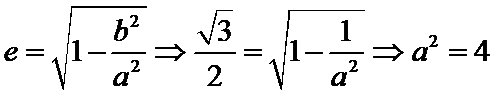
考查方向
解题思路
先根据抛物线与x轴的交点求出b的值,后利用离心率求出a的值;
易错点
不知道抛物线与x轴的交点即为b的值;
正确答案
(2)
解析
(Ⅱ)因为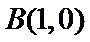
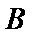
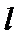
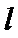
设直线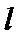
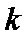
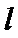
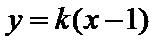
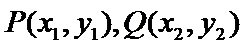
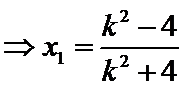
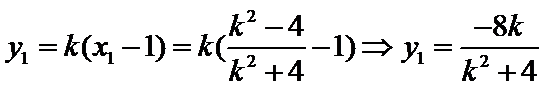
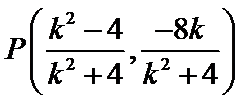
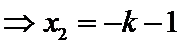
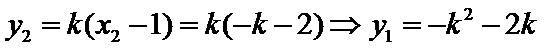
由
化简得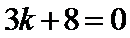
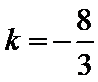
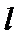
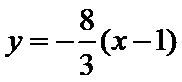
考查方向
解题思路
设出直线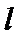
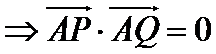
易错点
不会转化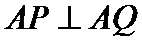
9.双曲线
正确答案


解析
试题分析:由双曲线

∵双曲线




考查方向
解题思路
根据双曲线的方程求出2c和渐近线方程。
易错点
注意双曲线中焦距为2c,双曲线的渐近线方程。
知识点
5.过双曲线

正确答案
解析
双曲线的右焦点为




考查方向
解题思路
先根据双曲线方程求出基本量后,将


易错点
将双曲线中的基本量与椭圆中的混淆导致出错;将
知识点
10.双曲线

正确答案
解析
由题意可知,双曲线的一个渐近线方程为:



考查方向
解题思路
先求出渐近线方程,代入抛物线方程,从而推出a和c的关系。
易错点
计算能力差
知识点
扫码查看完整答案与解析