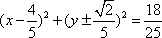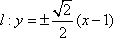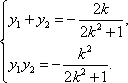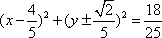直线的一般式方程
共52题

· 直线的一般式方程

直线的一般式方程
共52题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

已知点在抛物线上，直线R，且与抛物线

相交于两点，直线分别交直线于点.

（1）求的值；

（2）若，求直线的方程；

（3）试判断以线段为直径的圆是否恒过两个定点？若是，求这两个定点的坐标；若

不是，说明理由。

正确答案

见解析。

解析

（1）解：∵点在抛物线上， ∴.

解法1：（2）由（1）得抛物线的方程为.

设点的坐标分别为，依题意，，

由消去得，

解得.

∴.

直线的斜率，

故直线的方程为.

令，得，∴点的坐标为.

同理可得点的坐标为.

∴

∵， ∴.

由，得，

解得, 或,

∴直线的方程为，或.

（3）设线段的中点坐标为，

则

而，

∴以线段为直径的圆的方程为.

展开得.

令，得，解得或.

∴以线段为直径的圆恒过两个定点.

解法2：（2）由（1）得抛物线的方程为.

设直线的方程为，点的坐标为，

由解得

∴点的坐标为.

由消去，得，

即，解得或.

∴，.

∴点的坐标为.

同理，设直线的方程为，

则点的坐标为，点的坐标为.

∵点在直线上，

∴.

又，得，

化简得.

，

∵，

∴.

由，

得，

解得.

∴直线的方程为，或.

（3）设点是以线段为直径的圆上任意一点，

则，

得，

整理得，.

令，得，解得或.

∴ 以线段为直径的圆恒过两个定点.

知识点

直线的一般式方程抛物线的标准方程和几何性质直线与圆锥曲线的综合问题圆锥曲线中的探索性问题

题型：单选题

单选题 · 5 分

设O为坐标原点，,是双曲线（a＞0，b＞0）的焦点，若在双曲线上存在点P，满足∠P=60°，∣OP∣=,则该双曲线的渐近线方程为

Ax±y=0

Bx±y=0

Cx±=0

D±y=0

正确答案

解析

选D，本题将解析几何与三角知识相结合，主要考察了双曲线的定义、标准方程，几何图形、几何性质、渐近线方程，以及斜三角形的解法，属中档题

知识点

直线的一般式方程双曲线的几何性质

题型：简答题

简答题 · 12 分

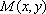
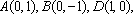
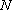
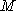
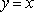
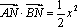
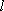
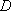
在平面直角坐标系中，已知动点，点点与点关于直线对称，且.直线是过点的任意一条直线。

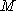
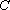
（1）求动点所在曲线的轨迹方程；

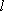
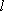
（2）设直线与曲线交于两点，且，求直线的方程；

（3）设直线与曲线交于两点，求以的长为直径且经过坐标原点的圆的方程。

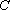
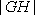
正确答案

（1）（2）（3）

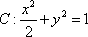
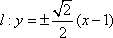
解析

（1）依据题意，可得点.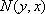

，

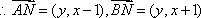
又，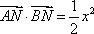

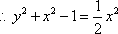
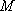
所求动点的轨迹方程为.

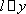
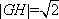
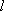
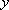
（2）若直线轴，则可求得，这与已知矛盾，因此满足题意的直线不平行于轴。

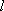
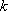
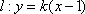
设直线的斜率为，则。

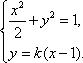
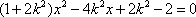
由得。

设点，有且恒成立（因点在椭圆内部）。

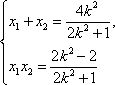
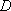
又，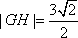

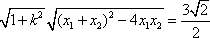
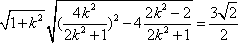
于是，，即，

解得。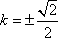

所以，所求直线

（3）当直线轴时，，点到圆心的距离为1.即点在圆外，不满足题意.

满足题意的直线的斜率存在，设为，则.

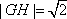
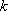
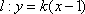
设点，由（2）知，进一步可求得

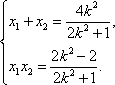
依据题意，有，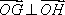

，

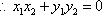
即，解得.

所求圆的半径，

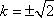
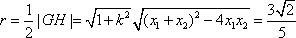
圆心为.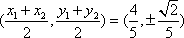

所求圆的方程为：

知识点

直线的一般式方程直线与圆锥曲线的综合问题直接法求轨迹方程直线、圆及圆锥曲线的交汇问题

题型：单选题

单选题 · 5 分

过点P(1,1)的直线将圆形区域{(x，y)|x2＋y2≤4}分为两部分，使得这两部分的面积之差最大，则该直线的方程为(　　)

Ax＋y－2＝0

By－1＝0

Cx－y＝0

Dx＋3y－4＝0

正确答案

解析

当OP与该直线垂直时，符合题意；此时kOP＝1，故所求直线斜率k＝－1.又已知直线过点P(1,1)，因此，直线方程为y－1＝－(x－1)，即x＋y－2＝0.

知识点

直线的一般式方程直线与圆的位置关系直线与圆相交的性质

题型：简答题

简答题 · 14 分

已知双曲线C的两个焦点坐标分别为，双曲线C上一点P到距离差的绝对值等于2.

（1）求双曲线C的标准方程；

（2）经过点M（2，1）作直线l交双曲线C的右支于A，B两点，且M为AB的中点，求直线l的方程.

（3）已知定点G（1，2），点D是双曲线C右支上的动点，求的最小值。

正确答案

见解析。

解析

（1）依题意，得双曲线C的实半轴长为a=1，焦半距为c=2，

所以其虚半轴长，

又其焦点在x轴上，所以双曲线C的标准方程为.

（2）设A、B的坐标分别为、，则

两式相减，得，

因为M（2，1）为AB的中点，所以，

所以，即.

故AB所在直线l的方程为，即.

（3）由已知，得，即，

所以，当且仅当三点共线时取等号.

因为，

所以，

故的最小值为.

知识点

直线的一般式方程双曲线的定义及标准方程双曲线的几何性质双曲线的相关应用直线与圆锥曲线的综合问题

继续学习学习下一知识点

下一知识点 : 直线的一般式方程与直线的平行关系

百度题库 > 高考 > 文科数学 > 直线的一般式方程

扫码查看完整答案与解析