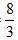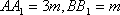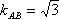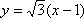- 排列、组合
- 共291题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设复数z满足(1-i)z=2i,则z=( )。
正确答案
解析


知识点
在实数集R中定义一种运算“△”,且对任意
①


则函数
正确答案
3
解析
略。
知识点
已知


(1)求函数
(2)求证:对于任意的

正确答案
见解析
解析
(1)函数


因为



当

所以,



(2)因为


又

所以,当

由

所以当


所以,当

所以,当
对于任意的



当



所以,当

所以,当
对于任意的



综上,对于任意的

知识点
已知函数f(x)=cosx(sinx+cosx)﹣
(1)若0<α<

(2)求函数f(x)的最小正周期及单调递增区间。
正确答案
(1)∵0<α<

∴cosα=
∴f(α)=cosα(sinα+cosα)﹣
=


=
(2)f(x)=cosx(sinx+cosx)﹣
=sinxcosx+cos2x﹣
=

=

∴T=
由2kπ﹣




∴f(x)的单调递增区间为[kπ﹣

解析
三角函数的图像与性质。
(1)利用同角三角函数关系求得cosα的值,分别代入函数解析式即可求得f(α)的值。
(2)利用两角和公式和二倍角公式对函数解析式进行恒等变换,进而利用三角函数性质和周期公式求得函数最小正周期和单调增区间。
知识点
已知以F为焦点的抛物线
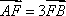
正确答案
解析
设BF=m,由抛物线的定义知
直线AB方程为
与抛物线方程联立消y得
所以AB中点到准线距离为
知识点
选修4-4:坐标系与参数方程
将圆
(1)写出C的参数方程;
(2)设直线



正确答案
(1)参数方程为 
(2)ρ=
解析
(1)在曲线C上任意取一点(x,y),由题意可得点(x,
∴x2+


(2)由


则线段P1P2的中点坐标为(
再根据与l垂直的直线的斜率为



再根据x=ρcosα、y=ρsinα 可得所求的直线的极坐标方程为ρcosα﹣2ρsinα+
即 ρ=
知识点
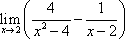
正确答案
解析
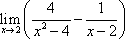
知识点
已知定点A(-1,0),F(2,0),定直线l:x=
(1)求E的方程;
(2)试判断以线段MN为直径的圆是否过点F,并说明理由。
正确答案
见解析
见解析。
解析
知识点
在复平面内,复数

正确答案
解析
略
知识点
扫码查看完整答案与解析