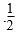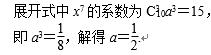二项式定理
共260题

二项式定理
共260题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 5 分

若的展开式中x4的系数为7，则实数a＝__________.

正确答案

解析

∵的通项为

，

∴8－r－＝4，解得r＝3.

∴，得.

知识点

求二项展开式的指定项或指定项的系数

题型：填空题

填空题 · 5 分

的二项展开式中的常数项为__________。

正确答案

解析

二项展开式的通项为，得r＝4，所以二项展开式的常数项为T5＝（－1）4＝15.

知识点

求二项展开式的指定项或指定项的系数

题型：简答题

简答题 · 12 分

甲乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛，若赛完5局仍未出现连胜，则判定获胜局数多者赢得比赛，假设每局甲获胜的概率为，乙获胜的概率为，各局比赛结果相互独立。

(1)求甲在4局以内（含4局）赢得比赛的概率；

(2)记为比赛决出胜负时的总局数，求的分布列和均值（数学期望）

正确答案

见解析。

解析

此题以古典概型和离散型随机变量分布列知识为背景，考察分析问题和解决问题的能力。

（1）p=

X可取值为2，3，4，5，其分布列为

∴E（X）=

知识点

求二项展开式的指定项或指定项的系数

题型：填空题

填空题 · 5 分

(x＋a)10的展开式中，x7的系数为15，则a＝________。(用数字填写答案)

正确答案

解析

知识点

求二项展开式的指定项或指定项的系数

题型：填空题

填空题 · 5 分

的二项展开式中的常数项为（）。（用数字作答）

正确答案

-160

解析

( -)6的展开式项公式是.由题意知，所以二项展开式中的常数项为

知识点

求二项展开式的指定项或指定项的系数

题型：简答题

简答题 · 13 分

已知函数

（1）当时，求曲线在点处的切线方程；

（2）求函数的极值。

正确答案

（1）；（2）当时，函数无极值

当时，函数在处取得极小值，无极大值

解析

函数的定义域为，。

（1）当时，，，

，

在点处的切线方程为，

即。

（2）由可知：

①当时，，函数为上的增函数，函数无极值；

②当时，由，解得；

时，，时，

在处取得极小值，且极小值为，无极大值。

综上：当时，函数无极值

当时，函数在处取得极小值，无极大值。

知识点

求二项展开式的指定项或指定项的系数

题型：填空题

填空题 · 4 分

设二项式的展开式中常数项为，则________。

正确答案

-10

解析

由，由已知得到：，所以，所以填-10

知识点

求二项展开式的指定项或指定项的系数

题型：填空题

填空题 · 5 分

的展开式中的系数为__________，（用数字作答）

正确答案

解析

通项,令得

,此时对应系数为.

知识点

求二项展开式的指定项或指定项的系数

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 二项式定理

扫码查看完整答案与解析