- 排列、组合
- 共291题
12.同时抛掷两枚质地均匀的硬币,当至少有一枚硬币正面向上时,就说这次试验成功,则在2次试验中成功次数X的均值是 .
正确答案
知识点
某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,. 学科&网现从这10人中随机选出2人作为该组代表参加座谈会.
(I)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;
(II)设

正确答案
试题解析:解:
所以,事件






所以,随机变量



知识点
16.某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,. 学科&网现从这10人中随机选出2人作为该组代表参加座谈会.
(I)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;
(II)设

正确答案
知识点
6.已知


正确答案
知识点
14.
正确答案
10
知识点
21.已知函数
(1)求
(2)


正确答案
解:(1)
令
①若



②若
方程


当
∴
③若


方程


此时

④若


此时的递增区间为
(2)问题等价于方程

而

令

再令
当





∴当


∴当



∴当
故当


解析
解析已在路上飞奔,马上就到!
知识点
7.若(ax2+
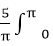

正确答案
2
解析
由于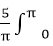

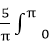

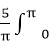



则(ax2+
Tr+1=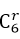

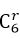
所以
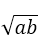
知识点
10.四面体的一条棱长为x,其余棱长为3,当该四面体体积最大时,经过这个四面体所有顶点的球的表面积为( )
正确答案
解析
底面积不变,高最大时体积最大,所以面BCD与面ABD垂直时体积最大,
由于四面体的一条棱长为x,其余棱长均为3,所以球心在两个正三角形的重心的垂线的交点,半径

考查方向
解题思路
先确定在哪一种结构下体积最大,然后再根据题目中的条件求解。
易错点
本题往往会因为不能准确地想象题目中所要求的空间几何体而无法求解。
知识点
14.已知


正确答案
解析
该二次项展开为






考查方向
解题思路
根据二项式展开式,求得
易错点
二项式展开后,忽略某几项乘积为
知识点
5.已知某一几何体的正视图与侧视图如图所示,则在下列图形中,可以是该几何体的俯视图的图形有( )
正确答案
解析
由正视图和侧视图知:俯视图的图形可以是①②③④,故选A.
知识点
扫码查看完整答案与解析
































