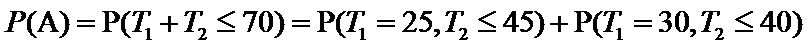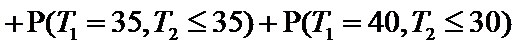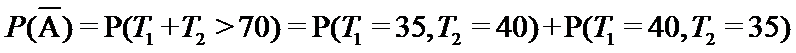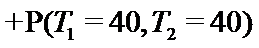- 排列、组合
- 共291题
11.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.计算:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设某校新、老校区之间开车单程所需时间为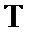
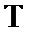
(1)求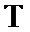
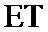
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
正确答案
(1)分布列为:
数学期望为32;
(2)0.91.
解析
试题分析:本题第(1)问属于用频率来估计概率的问题,难度不大;第(2)问是概率统计中的常见的和事件的概率问题,需要在计算的时候细心,第二问也可以从事件的对立面来考虑,利用互斥事件的概率公式求解。解题过程如下:
(I)由统计结果可得T的频率分步为
以频率估计概率得T的分布列为
从而 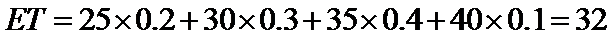
(II)设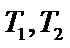

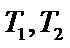
解法
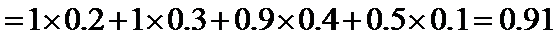
解法二:
故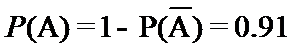
考查方向
解题思路
1、先根据频数分布表计算出对应的频率,在用频率估计概率,画出分布列,求出数学期望;
2、先找出“共用时间不超过120分钟”所蕴含的基本事件,然后再利用概率的加法公式求解;
易错点
本题容易因第(2)问不能分析出“共用时间不超过120分钟”所蕴含的含义而导致漏解或增解而出错;
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
函数
正确答案
解析
要使




知识点
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形。
(1)证明:PB⊥CD;
(2)求二面角A-PD-C的大小。
正确答案
见解析。
解析
(1)
证明:取BC的中点E,连结DE,则ABED为正方形。
过P作PO⊥平面ABCD,垂足为O.
连结OA,OB,OD,OE.
由△PAB和△PAD都是等边三角形知PA=PB=PD,
所以OA=OB=OD,即点O为正方形ABED对角线的交点,
故OE⊥BD,从而PB⊥OE.
因为O是BD的中点,E是BC的中点,
所以OE∥CD.因此PB⊥CD.
(2)解法一:由(1)知CD⊥PB,CD⊥PO,PB∩PO=P,
故CD⊥平面PBD.
又PD
取PD的中点F,PC的中点G,连结FG,
则FG∥CD,FG⊥PD.
连结AF,由△APD为等边三角形可得AF⊥PD.
所以∠AFG为二面角A-PD-C的平面角。
连结AG,EG,则EG∥PB.
又PB⊥AE,所以EG⊥AE.
设AB=2,则AE=

故AG=
在△AFG中,FG=

所以cos∠AFG=
因此二面角A-PD-C的大小为
解法二:
由(1)知,OE,OB,OP两两垂直。
以O为坐标原点,
设|


















设平面PCD的法向量为n1=(x,y,z),则n1·



n1·


可得2x-y-z=0,y+z=0.
取y=-1,得x=0,z=1,故n1=(0,-1,1)。
设平面PAD的法向量为n2=(m,p,q),则n2·





取m=1,得p=1,q=-1,故n2=(1,1,-1)。
于是cos〈n1,n2〉=
由于〈n1,n2〉等于二面角A-PD-C的平面角,所以二面角A-PD-C的大小为
知识点
如图11,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离表示成x的函数f(x),则y=f(x)在[0,π]上的图像大致为( )
正确答案
解析
根据三角函数的定义,点M(cos x,0),△OPM的面积为|sin xcos x|,在直角三角形OPM中,根据等积关系得点M到直线OP的距离,即f(x)=|sin xcos x|=|sin 2x|,且当x=时上述关系也成立, 故函数f(x)的图像为选项C中的图像。
知识点
设数列





(1)当

(2)当

正确答案
(1)3个;(2)393个
解析
(1)当


所以



所以满足条件的所有数列
(2)令


反之符合上述条件的7项数列
记符合条件的数列
显然




当



故
所以满足条件的所有数列
知识点
5.已知数列



正确答案
解析
由



考查方向
本题主要考察了排列组合的知识,属于中档题,是高考的热点,解决此类题的关键:找到

易错点
本题易在
知识点
扫码查看完整答案与解析