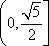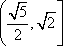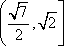- 排列、组合
- 共291题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知集合

正确答案
解析




知识点

正确答案
解析
方法一:
=
所以当

方法二:∵-6≤a≤3,∴3-a≥0,a+6≥0.
而(3-a)+(a+6)=9,
由基本不等式得:
(3-a)+(a-6)≥
即
∴
即
知识点
在平面上,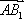

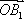
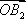
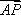
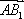
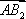



正确答案
解析
因为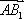
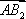
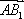
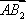
则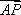

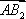
由|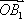
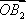
所以(x-a)2=1-y2≥0,(y-b)2=1-x2≥0.
由|


即0≤1-x2+1-y2<
所以
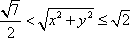
所以|
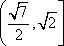
知识点
已知直线


(1)求实数
(2)若点



正确答案
(1) 
解析
知识点
已知圆







(1)求C的方程;
(2)



正确答案
(1) 
解析
由已知得圆





设动圆



(1)∵圆




由椭圆的定义可知,曲线C是以M,N为左右焦点,场半轴长为2,短半轴长为

(2)对于曲线C上任意一点



当且仅当圆P的圆心为(2,0)时,R=2.
∴当圆P的半径最长时,其方程为
当




当













当








当


综上,|AB|=
知识点
如图,在空间直角坐标系中有直三棱柱



正确答案
解析
设


则
知识点
设{an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和,记
(1)若c=0,且b1,b2,b4成等比数列,证明:Snk=n2Sk(k,n∈N*);
(2)若{bn}是等差数列,证明:c=0.
正确答案
见解析
解析
证明:由题设,
(1)由c=0,得

即
因此,对于所有的m∈N*,有Sm=m2a.
从而对于所有的k,n∈N*,有Snk=(nk)2a=n2k2a=n2Sk.
(2)设数列{bn}的公差是d1,则bn=b1+(n-1)d1,即

令A=

在(*)式中分别取n=1,2,3,4,得A+B+cd1=8A+4B+2cd1=27A+9B+3cd1=64A+16B+4cd1,
从而有
由②,③得A=0,cd1=-5B,代入方程①,得B=0,从而cd1=0.
即

若d1=0,则由
又因为cd1=0,所以c=0.
知识点
定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”,现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)=
正确答案
解析
由等比数列性质知
①
②

③

④f(an)f(an+2)=ln|an|ln|an+2|≠
故选C
知识点
现有某类病毒记作XmYn,其中正整数m,n(m≤7,n≤9)可以任意选取,则m,n都取到奇数的概率为__________。
正确答案
解析
由题意知m的可能取值为1,2,3,…,7;n的可能取值为1,2,3,…,9.由于是任取m,n:若m=1时,n可取1,2,3,…,9,共9种情况;同理m取2,3,…,7时,n也各有9种情况,故m,n的取值情况共有7×9=63种,若m,n都取奇数,则m的取值为1,3,5,7,n的取值为1,3,5,7,9,因此满足条件的情形有4×5=20种,故所求概率为
知识点
扫码查看完整答案与解析