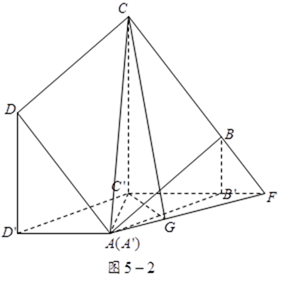- 直线方程和两条直线的位置关系
- 共650题
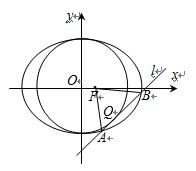
已知椭圆
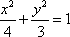
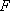
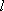
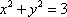
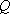
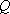
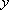
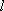
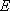
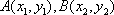
(1)若直线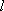
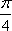
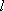
(2)求证: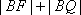
正确答案
见解析
解析
解析:(1)设直线
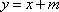
则有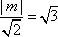
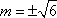
又切点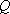
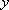

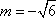
所以直线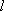

(2)因为
又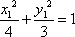
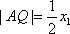
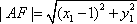
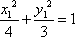
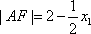
所以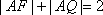
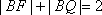
所以
知识点
如图,已知






(1)求异面直线

(2)求

正确答案
见解析
解析
(1)解法一:取



所以


由已知,

在


所以异面直线



解法二:如图所示建立空间直角坐标系,



所以异面直线


(2)





体积
知识点
如图1,在正三角形










(1)求证:

(2)若


(3)当



正确答案
见解析。
解析
(1)证明:






(2)解:若





即

(3)解:













即

以


则有






易知


设平面

由

∴
∴平面

知识点
如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点。
(1)求证:AF//平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求平面BCE与平面ACD所成锐二面角的大小。
正确答案
见解析。
解析
(1)取CE中点P,连结FP、BP,
∵F为CD的中点,∴FP//DE,且FP=
又AB//DE,且AB=
∴ABPF为平行四边形,∴AF//BP。 -------------------2分
又∵AF

∴AF//平面BCE。 -------------------4分
(2)∵△ACD为正三角形,∴AF⊥CD。
∵AB⊥平面ACD,DE//AB,
∴DE⊥平面ACD,又AF
∴DE⊥AF。又AF⊥CD,CD∩DE=D,
∴AF⊥平面CDE。 --------------------------------6分
又BP//AF,∴BP⊥平面CDE。又∵BP
∴平面BCE⊥平面CDE。 ------------------------8分
(3)法一、由(2),以F为坐标原点,FA,FD,FP所在的直线分别为x,y,z轴(如图),建立空间直角坐标系F—xyz,设AC=2,
则C(0,—1,0),

显然,
设面BCE与面ACD所成锐二面角为
则
即平面BCE与平面ACD所成锐二面角为45°,-----14分
法二、延长EB、DA,设EB、DA交于一点O,连结CO。
则
由AB的中位线,则
在




即平面BCE与平面ACD所成锐二面角为45°,-------------------------14分
知识点
已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A、D分别是RB、RC的中点,现将△RAD沿着AD折起到△PAD位置,使



(1)求证:

(2)求二面角
正确答案
见解析。
解析
解析:(1)∵点


∴ 
∴ ∠
∴ 


∴ 
∵ 
∴ 

∵ 

∴ 
(2)法一:
取



∵ 
∴ 
又由(1)知
而

∴ 
∵
∴ 

∴ ∠

在


在


∴ 
∴ 二面角

(2)法二:
建立如图所示的空间直角坐标系
则




设平面


令

∴ 
显然,



∴ cos<


∴ 二面角

知识点
如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF//AB,EH丄平面 ABCD,AB=2,EF=EH=1.
(1) 证明:平面ADF丄平面ABCD;
(2) 求五面体EF—ABCD的体积;
(3) 设N为EC的中点,若在平面ABCD内存在一点M,使MN丄平
面BCE,求MN的长。
正确答案
见解析。
解析
(1)
由题得
取

则


又



∴平面
(2)
在面

如图,则面

由(1)及

(3)
以G为原点,建立如图所示的空间直角坐标系则
设
若

得
知识点
如图5(1)中矩形













(1) 求证:
(2) 求

正确答案
见解析
解析
(1)由题设,M,N是矩形的边AD和BC的中点,所以AM



由AM=DM,可知△MAD是正三角形,所以AD=,在矩形ABCD中,AB=2,AD=


解(2)设E,F是BD,CD的中点,则EF


又BO=OD,所以



过A作AH⊥BD,由面面垂直的性质定理,可得AH⊥平面BOD,连结OH ,
所以OH是AO在平面BOD的投影,所以∠AOH为所求的角,即AO与平面BOD所成角。
AH是RT△ABD斜边上的高,所以AH=

所以sin∠AOH=
方法二:空间向量:取MD,NC中点P,Q,如图建系,
Q(0,0,0),B(


所以






(2)设平面BOD的法向量是





又




知识点
已知点


正确答案
解析


知识点
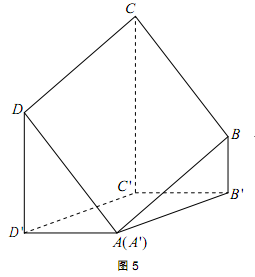
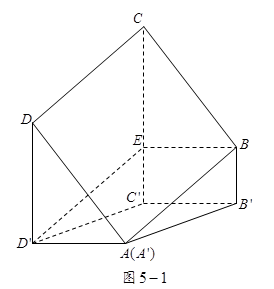
如图5,已知正方形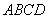
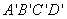
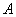
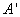

(1)证明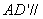
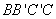
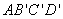
(2)如果四边形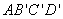
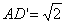
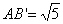
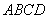
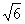
求平面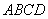
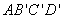
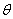
正确答案
见解析。
解析
(1)依题意,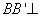
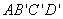
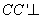
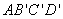
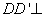
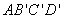
所以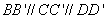
(法1)在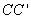
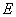
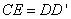
连结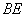

因为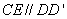
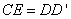
所以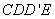

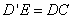
又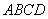
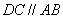
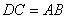
所以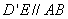
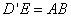
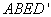
从而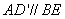
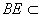
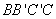
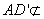
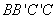
所以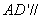
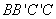
四边形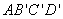
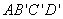
(法2)因为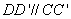
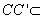
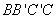
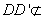
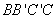
所以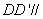
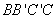
因为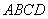
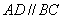
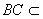
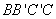
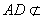
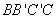
所以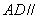
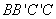
而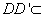
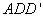
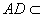
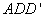
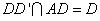
所以平面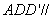
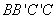
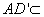

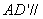
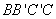
四边形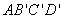
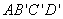
(2)依题意,在Rt△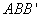
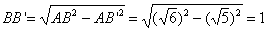
在Rt△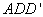
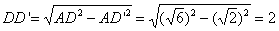
所以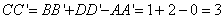
(注:或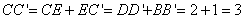
连结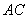
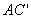
在Rt△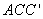
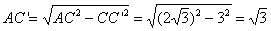
所以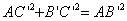
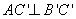
(法1)延长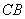
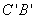
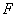
则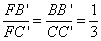
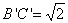
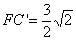
连结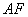
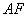
的交线。
在平面
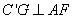
连结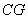
因为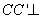
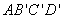
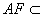
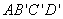
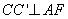
从而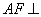
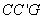
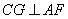
所以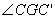
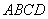
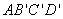
在Rt△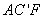
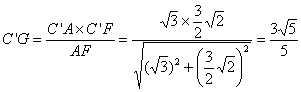
在Rt△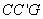
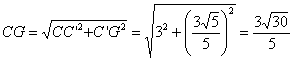
所以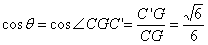
即平面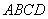
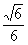
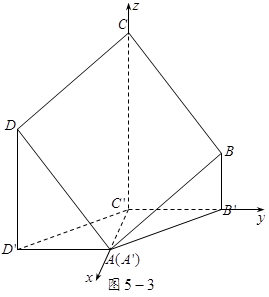
(法2)以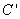
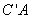
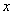
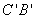
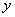
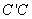
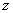
建立空间直角坐标系(如图5-3),
则平面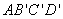
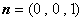
设平面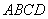
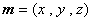
因为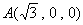
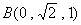
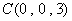
所以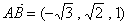
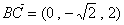
而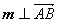
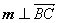
所以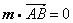
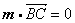
即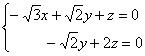
取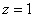
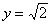
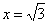
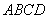
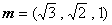
(注:法向量不唯一,可以是与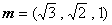
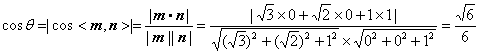
所以平面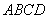
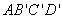
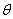
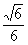
(法3)由题意,正方形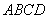
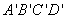
所以平面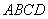
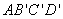
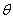
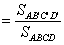
而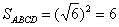
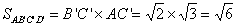
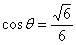
所以平面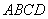
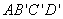
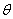
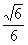
知识点
已知点


正确答案
解析
当P点同时满足(1)P为AB的中点;(2)P点到D点的距离最大时,AB取得最小值。P点的可行域如图所示,因为直线

知识点
扫码查看完整答案与解析