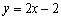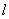- 直线方程和两条直线的位置关系
- 共650题
20.设圆
(I)证明
(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
正确答案
见解析
解析
(Ⅰ)因为


所以

又圆



由题设得





(Ⅱ)当





由

则

所以
过点













当





综上,四边形

知识点
11.已知O为坐标原点,F是椭圆C:
正确答案
知识点
22.如图,AB为圆O的直径,BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.
(Ⅰ)求证:BD平分∠CBE;
(Ⅱ)求证:
正确答案
见解析
解析
证明:
(I)由弦切角定理得到∠DBE=∠DAB,又∠DBC=∠DAC,∠DAB=∠DAC,所以∠DBE=∠DBC,即BD平分∠CBE.
(Ⅱ)由(I)可知BE=BH,所以
所以


考查方向
相似三角形 圆的相关概念与性质、角平分线的性质
解题思路
利用弦切角定理找出与其相等的角,并进行相等角间转化;利用相似三角形的判定定理判定△AHC∽△AEB;利用相似三角形对应边成比例,证明有关问题.
易错点
辅助线的作法,相似条件找不准
教师点评
找三角形相似的条件很重要
知识点
6.现有甲乙两船,其中甲船在某岛B的正南方A处,A与B相距7公里,甲船自A处以4公里/小时的速度向北方向航行,同时乙船以6公里/小时的速度自B岛出发,向北60o西方向航行,问_____分钟后两船相距最近?
正确答案
30
解析
解析已在路上飞奔,马上就到!
知识点
如图,PA是圆的切线,A是切点,M是PA的中点,过点M作圆的割线交圆于点C,B,连接PB,PC分别交圆于点E,F,EF与BC的交点为N.
30.求证:
31.
正确答案
证明略
解析
试题分析:本题属于平面几何问题,题目难度较低,解题时要注意深入分析已知条件和特征结论,善于将各已知条件联系起来考虑,寻找合理的解题思路。
由切割线定理,得
而
∴



又


考查方向
解题思路
本题考查三角形与圆的相关知识,解题步骤如下:
1、通过相应的条件和定理建立起有关角或边之间的关系式,如相似关系。
2、灵活运用圆的切割线定理及三角形相似得到所需结论。
易错点
1、未把中点M与切割线定理结合使用从而无法找到突破口;
2、第二问中由相似得到合适结论出错。
正确答案
证明略.
解析
试题分析:本题属于平面几何问题,题目难度较低,解题时要注意深入分析已知条件和特征结论,善于将各已知条件联系起来考虑,寻找合理的解题思路。
∵


又∵
∴


而

即
考查方向
本题考查了圆切割线定理及其应用,圆中圆周角等知识和性质,考查了三角形中的相似关系,意在考查考生处理几何问题的能力。
解题思路
本题考查三角形与圆的相关知识,解题步骤如下:
1、通过相应的条件和定理建立起有关角或边之间的关系式,如相似关系。
2、灵活运用圆的切割线定理及三角形相似得到所需结论。
易错点
1、未把中点M与切割线定理结合使用从而无法找到突破口;
2、第二问中由相似得到合适结论出错。
设双曲线C:


(1)求双曲线C的方程;
(2)求直线AB方程;
(3)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
正确答案
见解析。
解析
(1)依题意得
所以
故双曲线C的方程为
(2)设

两式相减得:
由题意得


所以

故直线AB的方程为
(3)假设A、B、C、D四点共圆,且圆心为P. 因为AB为圆P的弦,所以圆心P在AB垂直平分线CD上;又CD为圆P的弦且垂直平分AB,故圆心P为CD中点M.
下面只需证CD的中点M满足|MA|=|MB|=|MC|=|MD|即可。
由
由(1)得直线CD方程:
由




所以CD的中点M(-3,6).
因为



所以
即 A、B、C、D四点在以点M(-3,6)为圆心,
知识点
若存在实常数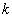
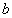
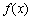
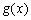
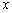
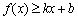
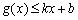
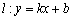
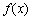
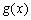
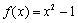
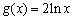
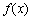
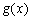
正确答案
解析
有题可知函数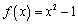
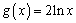
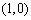
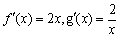
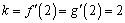
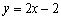
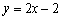
知识点
如图7,直线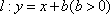
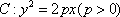
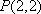
物线

(1)求直线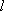
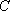
(2)过点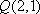
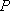
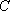
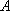

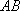
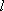
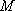
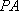
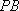
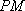
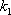
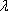
正确答案
见解析。
解析
(1)(法一)

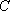
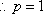
设与直线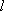
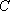
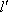
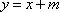
由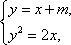
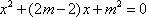
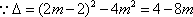

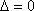
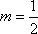
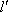
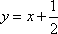

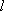


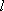

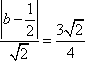

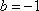


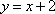

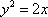
(法二)

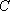
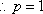


设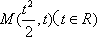
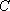
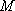
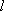

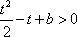
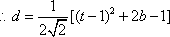
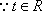
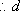
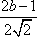
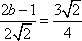
因此,直线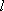
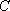
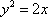
(2)
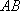

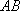
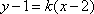

由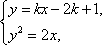
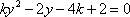
设点
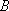
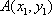
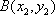
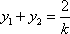

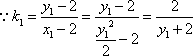

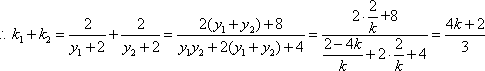
由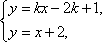
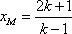
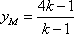
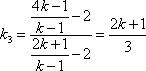
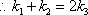
因此,存在实数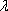
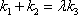
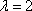
知识点
已知椭圆








(1)当








(2)是否存在实数

正确答案
(1)
解析
(1)①设椭圆的实半轴长为a,短半轴长为b,半焦距为c,
当

所以椭圆的方程为
②依题意知直线






设

则

因为


解得


(2)假设存在满足条件的实数






由







当

知识点
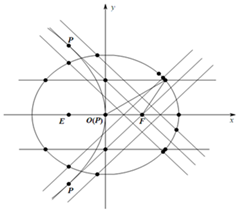
设椭圆
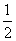
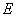
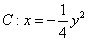
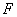
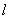
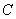
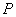
(1)求直线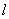
(2)椭圆上是否存在点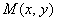
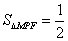
正确答案
见解析。
解析
(1)抛物线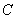
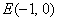
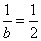
所以,
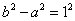

因此,所求椭圆的方程为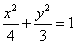
(2)椭圆的右焦点为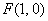
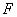
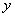
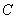


① 若
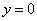
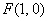
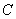
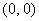
的方程为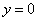
② 若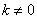

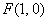
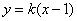
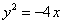
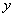
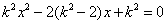
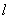
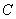
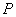
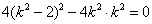
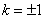
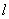
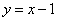


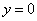
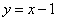

可求出点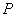
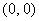
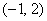
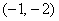
①若点
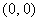
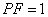
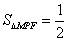
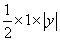

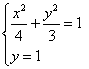
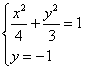
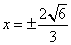
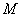
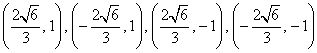
②若点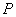
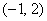
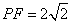
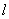
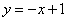
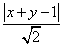
于是有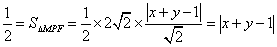
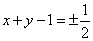
与(*)式联立: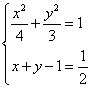

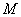
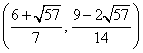
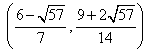


③ 若点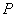
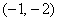
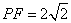
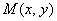

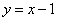
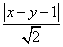
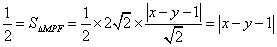
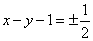
与(*)式联立: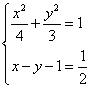

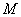
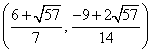
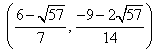
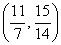
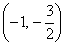
综合①②③,以上12个点各不相同且均在该椭圆上,因此,满足条件的点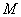
知识点
扫码查看完整答案与解析