- 互斥事件、对立事件的概率
- 共37题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
给出下列命题:
(1)已知事件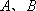
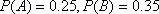
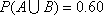
(2)已知事件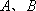
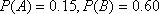
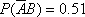
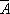
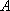
(3)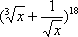
则其中真命题的序号是 [答]( )。
正确答案
解析
略
知识点
某工厂生产A,B两种元件,已知生产A元件的正品率为75%,生产B元件的正品率为80%,生产1个元件A,若是正品则盈利50元,若是次品则亏损10元;生产1个元件B,若是正品则盈利40元,若是次品则亏损5元。
(1)求生产5个元件A所得利润不少于140元的概率;
(2)设X为生产1个元件A和1个元件B所得总利润,求X的分布列和数学期望。
正确答案
见解析。
解析
知识点
在某班进行的演讲比赛中,共有
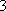

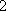
正确答案
60
解析
略
知识点
某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节,则在课程表上的相邻两节文化课之间最多间隔1节艺术课的概率为()(用数字作答)。
正确答案
解析
语文、数学、外语三门文化课排列,这三门课中间存在两个空,在两个空中,
若每个空各插入1节艺术课,则排法种数为 
若两个空中只插入1节艺术课,则排法种数为
若语文、数学、外语三门文化课相邻排列,则排法种数为
而所有的排法共有
故在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 

知识点
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-
(1)求角B的大小;
(2)若a+c=1,求b的取值范围。
正确答案
(1) 

解析
(1)由已知得-cos(A+B)+cos Acos B-
即有sin Asin B-
因为sin A≠0,所以sin B-
又cos B≠0,所以tan B=
又0<B<π,所以
(2)由余弦定理,有b2=a2+c2-2accos B.
因为a+c=1,cos B=

又0<a<1,于是有

知识点
如图,在正方体








正确答案
解析
直线



由于

所以
知识点
观察下列等式
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
……
照此规律,第n个等式可为__________。
正确答案
12-22+32-42+…+(-1)n+1n2=(-1)n+1·
解析
第n个等式的左边第n项应是(-1)n+1n2,右边数的绝对值为1+2+3+…+n=
知识点
已知函数


(1)


(2)


正确答案
见解析。
解析
(1)










(2)直接计算知
设函数
当


因为



当




由均值不等式知,




此时存在






知识点
扫码查看完整答案与解析




















