- 利用导数求函数的极值
- 共167题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
选修4-5:不等式选讲
设函数
(1)证明:
(2)若

正确答案
见解析。
解析
(1)由a>0,有f(x)=|x+1/a|+|x-a|≥|x+1/a-(x-a)|=1/a+a≥2.所以f(x)≥2.
(2)f(x)=|3+1/a|+|3-a|。
当a>3时,f(3)=a+1/a,由f(3)<5得3<a<
当0<a≤3时,f(3)=6-a+

综上所诉,a的取值范围为(
知识点
设函数f(x)=
正确答案
解析
略
知识点
已知函数


(1)若曲线



(2)求函数
(3)当



正确答案
见解析
解析
本小题主要考查函数与导数,函数的单调性、极值、零点等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、数形结合思想、分类与整合思想、化归与转化思想,满分14分。
(1)由

又曲线


得


(2)
①当




②当







所以


故


综上,当

当



(3)当
令
则直线


等价于方程

假设


又函数





又



所以

解法二:
(1)(2)同解法一。
(3)当

直线


等价于关于




在
①当


②当

令

令

当

当





从而

所以当
解得

综上,得

知识点
已知函数
(1) 求f(x)的反函数的图象上图象上点(1,0)处的切线方程;
(2)证明: 曲线y = f (x) 与曲线
(3)设a<b, 比较

正确答案
见解析
解析
(1) f (x)的反函数


(2) 证明曲线y=f(x)与曲线
因此,
所以,曲线y=f(x)与曲线
(3)设
令


所以
知识点
已知


(1)设函数F(x)=18f(x)-x2[h(x)]2,求F(x)的单调区间与极值;
(2)设

(3)设

正确答案
见解析
解析
(1)

令


当



故当






(2)方法一:原方程可化为
即为
①当






此时方程仅有一解
②当




若


若


若

方法二:原方程可化为
即
①当

②当

③当

④当

(3)由已知得

设数列



从而有


又

即对任意



则
知识点
已知函数f(x)=axsinx-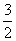
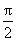
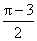
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,π)内的零点个数,并加以证明。
正确答案
(1) f(x)=xsinx-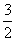
解析
(1)由已知得f′(x)=a(sinx+xcosx),
对于任意x∈(0,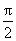
当a=0时,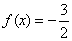
当a<0,x∈(0,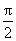
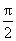
又f(x)在[0,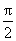
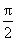
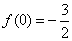
当a>0,x∈(0,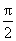
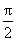
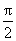
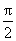
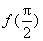
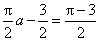
解得a=1。
综上所述,得f(x)=xsinx-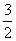
(2)f(x)在(0,π)内有且只有两个零点。
证明如下:
由(1)知,f(x)=xsinx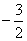
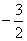
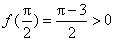
又f(x)在[0,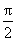
所以f(x)在(0,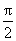
又由(1)知f(x)在[0,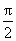
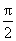
当x∈[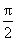
由g(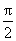
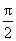
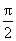
由g′(x)=2cosx-xsinx,知x∈(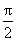
从而g(x)在(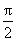
当x∈(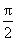
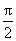
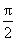
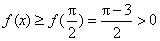
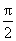
当x∈(m,π)时,有g(x)<g(m)=0,即f′(x)<0,从而f(x)在(m,π)内单调递减。
又f(m)>0,f(π)<0,且f(x)在[m,π]上的图象是连续不断的,从而f(x)在(m,π)内有且仅有一个零点。
综上所述,f(x)在(0,π)内有且只有两个零点
知识点
设函数



正确答案
解析
本题考查的是函数的极值,函数的极值不是最值,A错误;因为



知识点
已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(1)求a,b的值;
(2)讨论f(x)的单调性,并求f(x)的极大值。
正确答案
见解析
解析
(1)f′(x)=ex(ax+a+b)-2x-4.
由已知得f(0)=4,f′(0)=4.
故b=4,a+b=8.
从而a=4,b=4.
(2)由(1)知,f(x)=4ex(x+1)-x2-4x,
f′(x)=4ex(x+2)-2x-4=4(x+2)·
令f′(x)=0得,x=-ln 2或x=-2.
从而当x∈(-∞,-2)∪(-ln 2,+∞)时,f′(x)>0;
当x∈(-2,-ln 2)时,f′(x)<0.
故f(x)在(-∞,-2),(-ln 2,+∞)上单调递增,在(-2,-ln 2)上单调递减。
当x=-2时,函数f(x)取得极大值,极大值为f(-2)=4(1-e-2)。
知识点
已知函数f(x)=x2e-x.
(1)求f(x)的极小值和极大值;
(2)当曲线y=f(x)的切线l的斜率为负数时,求l在x轴上截距的取值范围。
正确答案
(1)极小值为f(0)=0;极大值为f(2)=4e-2.
(2)(-∞,0)∪[
解析
(1)f(x)的定义域为(-∞,+∞),
f′(x)=-e-xx(x-2),①
当x∈(-∞,0)或x∈(2,+∞)时,f′(x)<0;
当x∈(0,2)时,f′(x)>0.
所以f(x)在(-∞,0),(2,+∞)单调递减,在(0,2)单调递增。
故当x=0时,f(x)取得极小值,极小值为f(0)=0;
当x=2时,f(x)取得极大值,极大值为f(2)=4e-2.
(2)设切点为(t,f(t)),
则l的方程为y=f′(t)(x-t)+f(t)。
所以l在x轴上的截距为m(t)=
由已知和①得t∈(-∞,0)∪(2,+∞)。
令h(x)=

当x∈(-∞,-2)时,h(x)的取值范围是(-∞,-3)。
所以当t∈(-∞,0)∪(2,+∞)时,m(t)的取值范围是(-∞,0)∪[
综上,l在x轴上的截距的取值范围是(-∞,0)∪[
知识点
扫码查看完整答案与解析





























