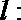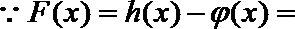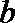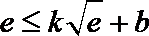- 利用导数求函数的极值
- 共167题
1
题型:简答题
|
21.设函数

(Ⅰ)当

(Ⅱ)若函数


(Ⅲ)若对于任意的



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
利用导数研究函数的单调性利用导数求函数的极值利用导数求函数的最值利用导数求参数的取值范围
1
题型:简答题
|
22.若存在实常数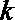
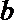
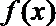
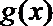
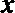
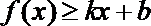
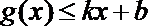
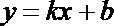
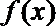
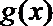
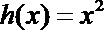
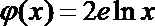
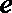
(1)求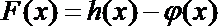
(2) 函数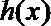
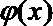
正确答案
(1) 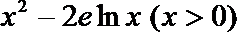
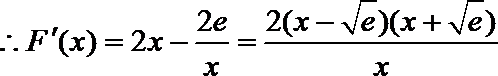

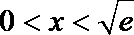
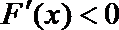
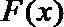
当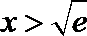
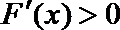
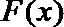
∴当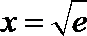
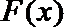
(2) 由(1)可知当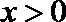
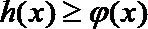

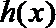
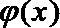
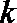

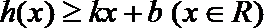
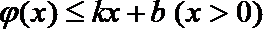
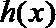
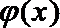

令
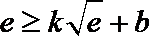
解析
解析已在路上飞奔,马上就到!
知识点
函数恒成立、存在、无解问题利用导数研究函数的单调性利用导数求函数的极值
1
题型:简答题
|
19.已知函数


(1)求
(2)求函数
正确答案
解:(1)
当

即
(2)
令
解析
解析已在路上飞奔,马上就到!
知识点
利用导数研究函数的单调性利用导数求函数的极值
1
题型:
单选题
|
9.设曲线





正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
利用导数求函数的极值
1
题型:
单选题
|
11.函数
正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
利用导数研究函数的单调性利用导数求函数的极值
下一知识点 : 利用导数求函数的最值
扫码查看完整答案与解析