- 利用导数求函数的极值
- 共167题
21.
设函数f(x)=ax2-a-lnx,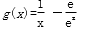
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)证明:当x>1时,g(x)>0;
(Ⅲ)确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立。
正确答案
知识点
6.已知a函数f(x)=x3-12x的极小值点,则a=( )
正确答案
知识点
12.已知函数




正确答案
解析



考查方向
解题思路
根据函数的导函数恒大于等于零最后转化为求函数的最值问题。
易错点
1、不能通过函数的导函数来解决问题。
知识点
9. 已知




正确答案
解析
设g(x)=lnx,h(x)=1/x-1,在同一坐标中它们表示的图象如图所示,
要使f(x)=g(x)-h(x)=0,即g(x)=h(x),即它们相交,交点的横坐标就是零点。从图中可以看到,令x=a,时,g(a)>h(a),即f(a)>0,同理可得,f(b)<0,因此此题选C
考查方向
解题思路
此题用图像法解答
易错点
函数零点的概念理解不透彻
知识点
11.若函数
正确答案
解析



考查方向
解题思路
先求出导函数,根据零点存在定理求出在(-1,2)上有极值点时k的范围,再取补集
易错点
区间(-1,2)上没有极值点误解为有极值点
知识点
19. 已知函数
(Ⅰ)当

(Ⅱ)若关于


正确答案
(Ⅰ)




(Ⅱ)

解析
(Ⅰ)函数


当

令

所以

所以





(Ⅱ)因为关于

令

所以
令

当




而

所以函数
当


所以

当


当



综上,当



法二:
因为关于

所以问题等价于方程
令

令
当


所以函数



所以函数
当


所以函数


当


当

所以函数
综上,当



法三:因为关于

所以问题等价于方程
设函数

令



所以函数


又当


所以函数

所以当


所以
考查方向
本题考查了利用导数求函数的单调性与极值,在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)求出函数

(Ⅱ)将方程解的问题转换为函数存在零点问题.
易错点
未注意到函数的定义域致误.
知识点
21.已知函数



(Ⅰ)若



(Ⅱ)设函数




(Ⅲ)令



正确答案
(Ⅰ)
(Ⅱ)
(Ⅲ)
解析
本题属于导数的基本问题,题目的难度是逐渐由易到难,
(1)直接按步骤来求,
(2)要注意分离参数;
(3)要注意讨论
(1)设


因为
且

切线方程为

当




(2)
由题意,得
即方程
令
则
所以






(3)因为

因为
所以




显然,当


则

又因为


由①②,得所求实数
考查方向
【考查方向】本题主要考查了导数的应用,导数的应用主要分以下几类:
1.利用导数的几何意义求切线方程,
2.利用导数研究函数的单调性、极值和最值或零点,
3.利用导数研究不等式恒成立或存在性。
易错点
1.第二问中,易忽视分离参数;
2.第三问中,易忽视“
知识点
21. 已知函数
(1)若
(2)若


(3)设b=0,若存在

正确答案
(1)

(2)
(3)
解析
试题分析:本题属利用导数求单调区间、最值及不等式恒成立问题,解析如下:
解:(1) 




所以


所以

(i) 若




故函数

此时
(ii)若

当





当


故
(3) 




因为

所以

因而



又
当


从而

所以



所以实数
考查方向
本题考查了利用导数求单调区间、最值及不等式恒成立问题。
易错点
第二问忘记分类讨论导致出错。
知识点
21.己知函数f(x)=a(x-
(1)若f(x)有极值,求a的取值范围;
(2)若f(x)有三个不同的零点x1,x2,x3,求证:
(参考数值:ln2≈0. 6931)
正确答案
(1)0<a<1;(2)当a≤0或a≥1时,

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)要注意对参数的讨论.
(1)
所以ax2-2x+a=0有正根且不为等根。显然a≠0,由x1x2=1>0.得Δ>0且x1+x2>0,
所以 0<a<1 。
考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:(1)根据判别式讨论;(2)根据二次函数的根的大小;3、定义域由限制时,根据定义域的隐含条件;4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;5、多次求导求解等.
解题思路
本题考查导数的性质,解题步骤如下:
(1)求导,然后解导数不等式,算极值。
(2)对参数分类讨论求得零点个数。
易错点
第二问中的易丢对a的分类讨论。
知识点
20.已知

(1)讨论函数
(2)若函数

①求实数
②求证:
正确答案
见解析
解析
(1)


①当


②当




所以


(2)①由(I)知,当


当







所以

此时,

令

所以


所以
②证法一:
下面证明:当

设





即当






②证法二:
令
则:
所以函数



于是
又

考查方向
解题思路
1利用导数求函数单调性,2根据函数的零点求参数的取值范围
3构造函数求两个零点和的范围
易错点
本题必须注意函数的定义域,以及对参数进行讨论,否则求解错误。
知识点
扫码查看完整答案与解析


















































