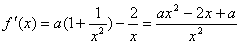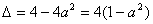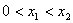- 利用导数求函数的极值
- 共167题
已知

正确答案
解析
略
知识点
已知函数


(1)若函数


(2)函数


正确答案
见解析。
解析
解:
∵函数


又

(1)函数


解得
所以
(2)因为函数

在区间
则


知识点
设函数
(1)若函数
(2)当a=1时,求函数
正确答案
见解析。
解析
(1)∵
∴
令
当x变化时,

故函数
因此



解得

(2)当a=1时,


①当t+3<-1,即t<-4时,
因为


②当

因为





由





③当t+3>2,即t>-1时,
由②得







综上所述,当a=1时,


知识点
正确答案
见解析。
解析
结合①可知
所以,x1=是极小值点,x2=是极大值点。
(2)若f(x)为R上的单调函数,则f′(x)在R上不变号,结合①与条件a>0,知ax2-2ax+1≥0在R上恒成立,因此Δ=4a2-4a=4a(a-1)≤0,由此并结合a>0,知0<a≤1。
知识点
已知函数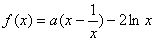
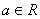
(1)若a=1,判断函数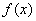
(2)求函数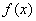
(3)设函数
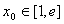
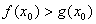
正确答案
见解析。
解析
(1)当
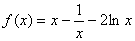
因为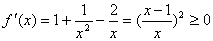
所以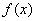
所以函数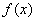
(2)函数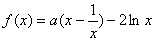
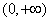
当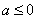
因为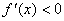
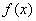
当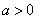
当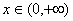
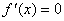
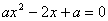
①当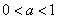
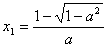
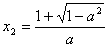
因为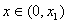
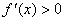
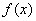
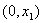
因为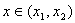
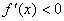
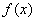
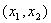
因为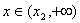
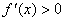
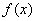
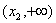
②当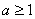
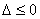
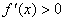
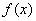
综上,当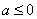
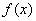
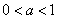
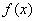
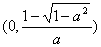
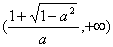
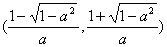
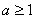
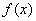
(3)由存在一个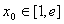
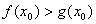
得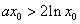

令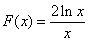
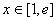
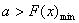
因为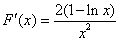
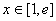
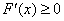
所以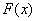
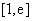
故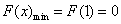
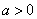
知识点
扫码查看完整答案与解析