利用导数求函数的极值
共167题

· 利用导数求函数的极值

利用导数求函数的极值
共167题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

已知函数单调递减。

（1）求a的值；

（2）是否存在实数b，使得函数的图象恰有3个交点，若存在，请求出实数b的值；若不存在，试说明理由。

正确答案

见解析。

解析

（１）由函数

单调递减知。

，。

（２）函数的图象恰好有3个交点，等价于方程

。

是其中一个根，

故存在实数：满足题意。

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数求函数的最值

题型：简答题

简答题 · 14 分

已知函数。

（1）若在处取得极值，求实数的值；

（2）求函数在区间上的最大值。

正确答案

见解析。

解析

（1）因为，

所以函数的定义域为。

且，

因为在处取得极值，

所以。

解得，

当时，，

当时，；当时，；当时，。

所以是函数的极小值点。

故。

（2）因为，

所以，

由（1）知。

因为，所以。

当时，；当时，。

所以函数在上单调递增；在上单调递减。

①当时，在上单调递增，

所以。

②当即时，在上单调递增，在上单调递减，

所以，

③当，即时，在上单调递减，

所以。

综上所述：

当时，函数在上的最大值是；

当时，函数在上的最大值是，

知识点

利用导数求函数的极值利用导数求函数的最值

题型：单选题

单选题 · 5 分

函数的定义域为（）

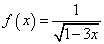
正确答案

解析

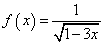
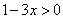
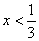
要使函数有意义，需使，解得。

知识点

利用导数求函数的极值

题型：简答题

简答题 · 12 分

已知实数a满足1＜a≤2，设函数f (x)＝x3－x2＋ax。

（1）当a＝2时，求f (x)的极小值；

（2）若函数g(x)＝4x3＋3bx2－6(b＋2)x (b) 的极小值点与f (x)的极小值点相同，求证：g(x)的极大值小于等于10。

正确答案

见解析。

解析

(1) 解：当a＝2时，f ′(x)＝x2－3x＋2＝(x－1)(x－2)，列表如下：

所以f (x)的极小值为f (2)＝

(2) 证明：。

由于a＞1，

所以f (x)的极小值点为x＝a，则g(x)的极小值点也为x＝a。

而，

所以，即b＝－2(a＋1)。

又因为1＜a≤2，所以g(x)极大值＝g(1)＝4＋3b－6(b＋2)＝－3b－8＝6a－2≤10.

故g(x)的极大值小于等于10。

知识点

利用导数求函数的极值

题型：简答题

简答题 · 13 分

已知函数，其中且.

（1）求证：函数在点处的切线与总有两个不同的公共点；

（2）若函数在区间上有且仅有一个极值点，求实数的取值范围。

正确答案

见解析

解析

（1）由已知可得. ------------------1分

， ------------------2分

又

在处的切线方程为. --------------------4分

令，整理得.

或， ------------------5分

， --------------------6分

与切线有两个不同的公共点. -----------------------7分

（2）在上有且仅有一个极值点，

在上有且仅有一个异号零点， -------------9分

由二次函数图象性质可得， ------------------------10分

即，解得或， ---------------12分

综上，的取值范围是. -------------------13分

知识点

导数的几何意义利用导数求函数的极值

继续学习学习下一知识点

下一知识点 : 利用导数求函数的最值

百度题库 > 高考 > 文科数学 > 利用导数求函数的极值

扫码查看完整答案与解析