利用导数求函数的极值
共167题

· 利用导数求函数的极值

利用导数求函数的极值
共167题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

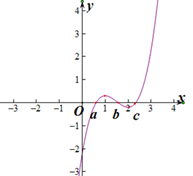
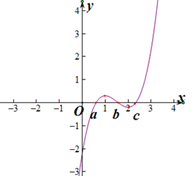
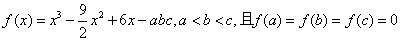
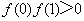
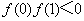
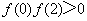
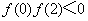
已知，现给出如下结论：①；②；③；④.其中正确结论的序号为：

A①③

B①④

C②④

D②③

正确答案

解析

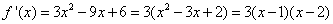
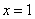
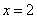
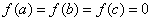
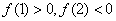
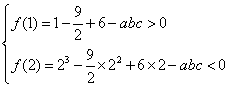
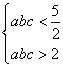
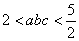
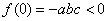
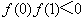
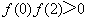
函数的导数为。则函数在处取得极大值，在处取得极小值，因为，所以函数有3个零点，则，即，解得，即，所以，所以，.所以选D.

知识点

命题的真假判断与应用利用导数求函数的极值

题型：简答题

简答题 · 12 分

已知函数在处取得极值。

（1）求实数的值；

（2）若关于的方程在区间上恰有两个不同的实数根，求实数的取值范围。

正确答案

见解析。

解析

（1）.

∵时，取得极值，∴.

故，解得.

经检验符合题意，∴.

（2）知，由，得

，令，则

在上恰有两个不同的实数根等价于

在上恰有两个不同实数根。

当时，，于是在上单调递增；

当时，，于是在上单调递减.

依题意有，

解得，

∴实数的取值范围是.

知识点

利用导数求函数的极值利用导数求参数的取值范围

题型：简答题

简答题 · 14 分

设函数的图象关于原点对称，的图象在点处的切线的斜率为-6，且当时有极值。

（1）求的值；

（2）求的所有极值。

正确答案

见解析。

解析

（1）由函数的图象关于原点对称，得，

∴，∴，

∴，即，

∴。

（2）由（1）知，∴。

由，∴，

∴，

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的极值

题型：简答题

简答题 · 14 分

已知函数。

（1）求函数的最大值；

（2）求函数在区间上的零点的个数（为自然对数的底数）；

（3）设函数图象上任意不同的两点为、，线段的中点为，记直线的斜率为，证明：。

正确答案

见解析。

解析

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数求函数的最值利用导数证明不等式

题型：填空题

填空题 · 5 分

若变量 x , y满足约束条件表示平面区域M，则平面区域M的面积是________;当 —4时，动直线所经过的平面区域M的面积为_____________.

正确答案

8 , 7

解析

略

知识点

利用导数求函数的极值

题型：简答题

简答题 · 14 分

已知函数，。

(1)若不等式在区间 ()内的解的个数；

(2)求证：。

正确答案

见解析。

解析

(1) 由，得。

令所以，方程在区间内解的个数即为函数的图像与直线交点的个数。

当时, .

当在区间内变化时, , 变化如下:

当时，；当时，；当时，。

所以，　（i）当或时，该方程无解

（ii）当或时，该方程有一个解；

（iii）当时，该方程有两个解。

(2) 由(1)知，∴.

∴. -

∴

∴.

∵.

∴ .

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数证明不等式

题型：简答题

简答题 · 12 分

已知函数是常数，且当和时，函数取得极值

（1）求函数的解析式；

（2）若曲线与有两个不同的交点，求实数的取值范围

正确答案

见解析。

解析

（1），

依题意，即解得

∴

（2）由（1）知，曲线与有两个不同的

交点，即在上有两个不同的实数解…5分

设，则，

由0的或

当时，于是在上递增；

当时，于是在上递减.

依题意有.

∴实数的取值范围是.

知识点

利用导数求函数的极值利用导数求参数的取值范围

题型：简答题

简答题 · 13 分

设，函数。

（1）若是函数的极值点，求实数的值；

（2）若函数在上是单调减函数，求实数的取值范围。

正确答案

见解析

解析

（1）。

因为是函数的极值点，所以，即，

所以，经检验，当时，是函数的极值点。

即。-----------------6分

（2）由题设，，又，

所以，，，

这等价于，不等式对恒成立。

令（），

则，---------------10分

所以在区间上是减函数，

所以的最小值为。--------------12分

所以，即实数的取值范围为。---------------13分

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数求参数的取值范围

题型：单选题

单选题 · 5 分

已知，现给出如下结论：①；②；③；④.其中正确结论的序号为：

A①③

B①④

C②④

D②③

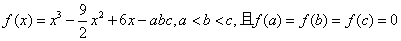
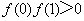
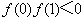
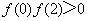
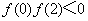
正确答案

解析

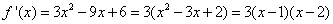
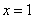
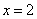
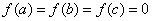
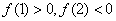
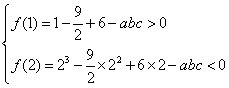
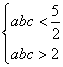
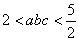
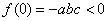
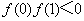
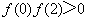
函数的导数为。则函数在处取得极大值，在处取得极小值，因为，所以函数有3个零点，则，即，解得，即，所以，所以，.所以选D.

知识点

函数零点的判断和求解利用导数研究函数的单调性利用导数求函数的极值

题型：单选题

单选题 · 5 分

若直线平分圆的周长，则的取值范围是

正确答案

解析

依题意知直线过圆C的圆心（-1,2），即，由，故选B.

知识点

利用导数求函数的极值

继续学习学习下一知识点

下一知识点 : 利用导数求函数的最值

百度题库 > 高考 > 文科数学 > 利用导数求函数的极值

扫码查看完整答案与解析