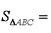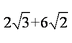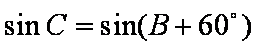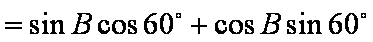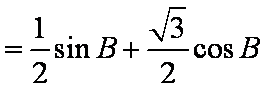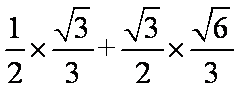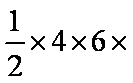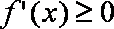- 利用导数求函数的极值
- 共167题
因客流量临时增大, 某鞋店拟用一个高为50㎝(即











(1) 当



(2) 当顾客的鞋



正确答案
见解析
解析
解: (1)因为




同理,由

所以
因为


故当

另法: 可得


所以



(2)由






从而



知识点
已知实数a、b、c、d成等比数列,且函数
正确答案
解析
y′=-1,令y′=0得x=-1,当-2<x<-1时,y′>0,当x>-1时,y′<0,∴b=-1,c=ln(-1+2)-(-1)=1,∴ad=bc=-1,故选A
知识点
设函数
(1)设
(2)若

正确答案
见解析。
解析
(1)
∵

(a)当


故

(b)当
①当



②当



∴


综上当

当


(2)由题(1)知,

………………………………………………………………………………………9分
∵



∵
∴

故

知识点
已知函数

(1)求实数
(2)若



(3)当

正确答案
见解析
解析
(1)
令
故


(2)当

令



由于



则









(3)要证
即证 

令
又





知识点
设函数
(1)若



(2)若

正确答案
见解析。
解析
(1)



又





由

又




(2)若






化为



知识点
已知函数f(x)=x2ln|x|,
(1)判断函数f(x)的奇偶性;
(2)求函数f(x)的单调区间;
(3)若关于x的方程f(x)=kx﹣1有实数解,求实数k的取值范围。
正确答案
见解析。
解析
(1)函数f(x)的定义域为{x|x∈R且x≠0}
f(﹣x)=(﹣x)2ln|﹣x|=x2lnx=f(x)
∴f(x)为偶函数
(2)当x>0时,
若
若
递增区间是

递减区间是

(3)要使方程f(x)=kx﹣1有实数解,即要使函数y=f(x)的图象与直线y=kx﹣1有交点。
函数f(x)的图象如图。
先求当直线y=kx﹣1与f(x)的图象相切时k的值。
当k>0时,f'(x)=x•(2lnx+1)
设切点为P(a,f(a)),则切线方程为y﹣f(a)=f'(a)(x﹣a),
将x=0,y=﹣1代入,得﹣1﹣f(a)=f'(a)(﹣a)
即a2lna+a2﹣1=0(*)
显然,a=1满足(*)
而当0<a<1时,a2lna+a2﹣1<0,
当a>1时,a2lna+a2﹣1>0
∴(*)有唯一解a=1
此时k=f'(1)=1
再由对称性,k=﹣1时,y=kx﹣1也与f(x)的图象相切,
∴若方程f(x)=kx﹣1有实数解,则实数k的取值范围是(﹣∞,﹣1]∪[1,+∞)。
知识点
在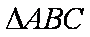
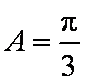
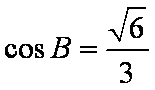
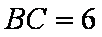
(1)求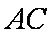
(2)求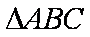
正确答案
(1)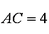
解析
(1)因为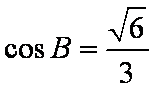

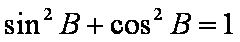
所以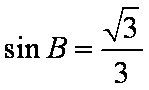
由正弦定理得,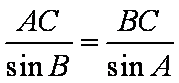
所以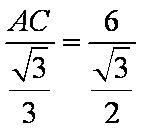
所以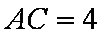
(2)在
=
=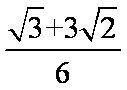
所以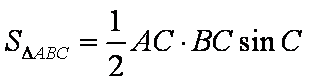
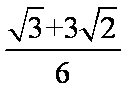
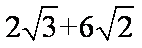
知识点
已知函数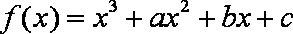
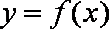
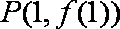
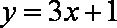
(1)若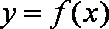
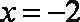
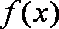
(2)若函数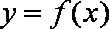
正确答案
见解析。
解析
(1)由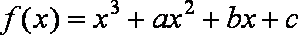
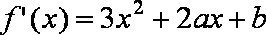
过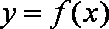
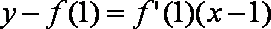
即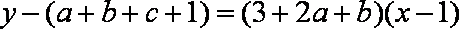
而过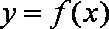
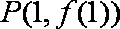
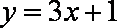
故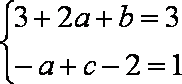
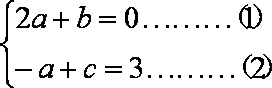
因为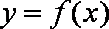
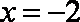
故
由(1)(2)(3)联立解得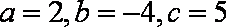
所以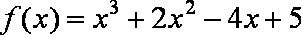
(2)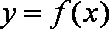
又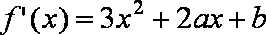
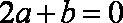
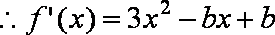
依题意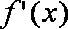
即
①在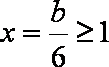
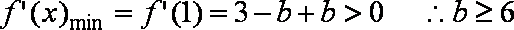
②在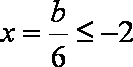
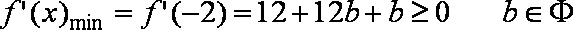
③在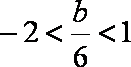
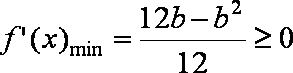
综合上述讨论可知,所求参数b的取值范围是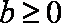
知识点
已知函数
(1)若函数

(2)若对任意给定的
使得
正确答案
见解析。
解析
(1)因为



令












(2)







当
当







此时,当
又因为,当








令













综合①④可知,当
在

知识点
已知平面上的动点


(1)求动点

(2)过点




求直线
(3)试问在曲线





两点,使得

正确答案
见解析。
解析
(1)设

化简得曲线

(2)设

由 

令直线AB方程为
由
则
由 ①和
代入
依题意直线AB的斜率大于0,即 

故直线AB的方程为
(3)设



切线


则切线

由

又


设
得
所以
故存在点

知识点
扫码查看完整答案与解析