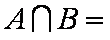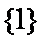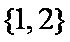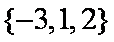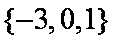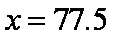- 利用导数求函数的极值
- 共167题
已知

(1)若


(2)求
(3)设



正确答案
见解析
解析
(1) 


经检验, 
(2) 
(i)当


(ii)当

① 若




② 若



综上所述,当


当



(3)当


易知


注意到
故由题设知

故

知识点
集合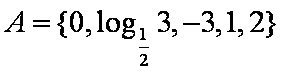

正确答案
解析
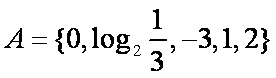
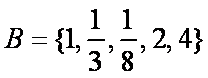
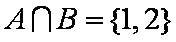
知识点
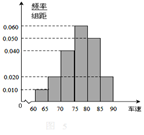
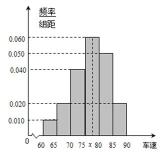
2013年春节期间,高速公路车辆较多。某调查公司在太原从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(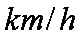
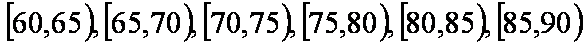
(1)某调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数和中位数的估计值.
(3)若从车速在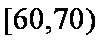
正确答案
见解析
解析
(1)系统抽样
(2)众数的估计值为最高的矩形的中点,即众数的估计值等于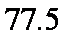
设图中虚线所对应的车速为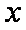
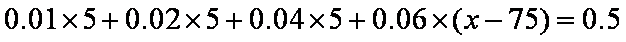
即中位数的估计值为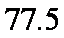
(3)从图中可知,车速在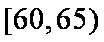
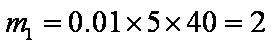
车速在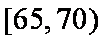
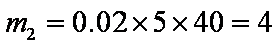
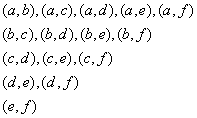
设车速在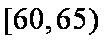

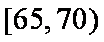
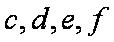
其中车速在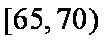
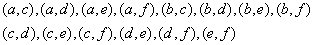
所以,车速在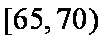
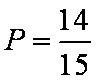
知识点
某次素质测试,随机抽取了部分学生的成绩,得到如图所示的频率分布直方图。
(1)估计成绩的平均值;
(2)若成绩排名前5的学生中,有一人是学生会主席,从这5人中推荐3人参加自主招生考试,试求这3人中含该学生会主席的概率。
正确答案
见解析
解析
(1)组距为10,各组的频率分别为0.12,0.18,0.4,0.22,0.08.
分数的平均值
(2)记学生会主席为A,其余四人为1,2,3,4. 五人中任推三人,基本事件为:
(A,1,2)(A,1,3) (A,1,4) (A,2,3) (A,2,4) (A,3,4)
(1,2,3) (1,2,4) (1,3,4) (2,3,4) 共10个.
满足要求的有6个,记所求事件为M,
知识点
已知正ΔABC边长为3,












(1)求
(2)求数列
正确答案
见解析。
解析
(1)BPn=an,BPn+1=an+1,则BPn=0.5an,QnC=3-0.5an,CRn=1.5-0.25an,
ARn=1.5+0.25an,APn+1=0.75+0.125an,BPn+1=
(2)由





则
令
所以
知识点
扫码查看完整答案与解析