- 古典概型与几何概型
- 共333题
从3名男同学,2名女同学中任选2人参加体能测试,则选到的2名同学中至少有一名男同学的概率是
正确答案
解析
略
知识点
某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题。
(1)求全班人数及分数在
(2)估计该班的平均分数,并计算频率分布直方图中
(3)若要从分数在

正确答案
见解析。
解析
(1)由茎叶图知,分数在


全班人数为
所以分数在
(2)分数在

分数在

分数在

分数在

分数在

所以,该班的平均分数为
估计平均分时,以下解法也给分:
分数在

分数在

分数在

分数在

分数在

所以,该班的平均分约为
频率分布直方图中

(3)将



















其中,至少有一个在

故至少有一份分数在

知识点
某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足

(1)求该学生考上大学的概率;
(2)如果考上大学或参加完5次考试就结束,求该生至少参加四次考试的概率。
正确答案
见解析。
解析
(1)记“该生考上大学”的事件为

则

(2)记“该生参加测试的次数”为



知识点
将一颗质地均匀的骰子连续投掷两次,朝上的点数依次为



正确答案
解析
略
知识点
对某校高三年级学生参加社区服务次数进行统计,随机抽取

(1)求出表中

(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
正确答案
见解析
解析
(1)由分组



所以
因为频数之和为



因为


(2)因为该校高三学生有240人,分组

所以估计该校高三学生参加社区服务的次数在此区间内的人数为
(3)这个样本参加社区服务的次数不少于20次的学生共有
设在区间



则任选


而两人都在

所以所求概率为

知识点
正确答案
见解析
解析
(1)由频率分布表得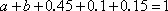
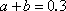
因为抽取20件日用品中,等级系数为2的恰有4件,所以
解得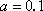
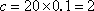
从而
所以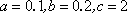
(2) 从日用品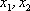
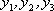
………9分
设事件A表示“从日用品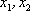
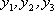
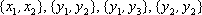
故所求的概率 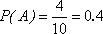
知识点
一个盒子中装有标号为1,2,3,4的4张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相邻整数的概率:
(1) 标签的选取是无放回的;
(2) 标签的选取是有放回的。
正确答案
见解析。
解析
解: (1) 无放回地从4张标签随机地选取两张标签的基本事件有{1,2},{1,3},{1,4}, {2,3},{2,4}, {3,4},总数为2×6个
两张标签上的数字为相邻整数基本事件为{1,2},{2,3},{3,4}总数为2×3个
∴P=
(2) 有放回地从4张标签随机地选取两张标签的基本事件有{1,2},{1,3},{1,4}, {2,3},{2,4}, {3,4},和(1,1),(2,2),(3,3),(4,4),总数为2×6+4=16个
两张标签上的数字为相邻整数基本事件为{1,2},{2,3},{3,4}总数为2×3个
P=
知识点
为了了解甲、乙两名同学的数学学习情况,对他们的7次数学测试成绩(满分100分)进行统计,作出如下的茎叶图,其中
(1)求

(2)现从成绩在[90,100]之间的试卷中随机抽取两份进行分析,求恰抽到一份甲同学试卷的概率。
正确答案
见解析
解析
(1)




(2)甲同学成绩在[90,100]之间的试卷有二份,分别记为

乙同学成绩在[90,100]之间的试卷有三份,分别记为


“从这五份试卷中随机抽取两份试卷”的所有可能结果为:









记“从成绩在[90,100]之间的试卷中随机抽取两份,恰抽到一份甲同学试卷”为事件






则
答:从成绩在[90,100]之间的试卷中随机抽取两份进行分析,恰抽到一份甲同学试卷的概率为
知识点
《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在+20—80mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属于碎酒驾车,某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾驶员共20人,检测结果如下表:
(1)求检测数据中醉酒驾驶的频率;
(2)估计检测数据中酒精含量的平均数。
正确答案
见解析
解析
(1)所求频率为
(2)估计所求平均数为

知识点
从1,2,3,4,5,6这六个数中,随机抽取2个不同的数,则这2个数的和为偶数的概率是 .
正确答案
解析
解析:从1,2,3,4,5,6这六个数中,随机抽取2个不同的数,基本事件有:
(1,2)(1,3)(1,4)(1,5)(1,6)(2,3)(2,4)(2,5)(2,6)(3,4)(3,5)(3,6)(4,5)(4,6)(5,6),共15个,其中“和为偶数”包括的基本事件有:(1,3)(1,5)(2,4)(2,6)(3,5)(4,6),共6个,所以其概率为:
故答案为:
知识点
扫码查看完整答案与解析