- 古典概型与几何概型
- 共333题
口袋中有形状、大小都相同的3只白球和1只黑球,现一次摸出2只球,则摸出的两球颜色不相同的概率是
正确答案
解析
略
知识点
“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动,假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(1)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构

根据表中数据,能否有90%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附:
正确答案
见解析
解析
(1)这3个人接受挑战分别记为

这3个人参与该项活动的可能结果为:







其中,至少有2个人接受挑战的可能结果有:




(2)根据


因为
知识点
甲、乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别为


正确答案
解析
略
知识点
某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过






(1)若甲停车





(2)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为
正确答案
(1)
解析
解析:
(1)解:设“甲临时停车付费恰为

则 


(2)解:设甲停车付费


则甲、乙二人的停车费用构成的基本事件空间为:


其中,

故“甲、乙二人停车付费之和为

知识点
将一个质地均匀,且四个面标有2、3、4、9四个数字的正四面体先后抛掷两次,观察四面体落在水平桌面后底面上的数字。
(1)求两数之和为奇数的概率;
(2)以第一次的数字为底数,第二次的数字为真数,构造一个对数,在所有的对数构成的集合中任取一个数,求该数大于1的概率。
正确答案
见解析。
解析
(1)将四面体先后抛掷两次,所得数字构成有序实数对作为一个基本事件,基本事件空间
两数之和为奇数的有8个,所以概率为
(2)所有的对数构成的集合为

则任取一个数字大于1的概率为
知识点
书架上有语文书,数学书各三本,从中任取两本,取出的恰好都是数学书的概率为 ( )
正确答案
解析
略
知识点
某城市随机抽取一个月(30天)的空气质量指数
(1)根据以上数据估计该城市这30天空气质量指数
(2)若该城市某企业因空气污染每天造成的经济损失


若在本月30天中随机抽取一天,试估计该天经济损失
正确答案
(1)175(2)
解析
解析:(1)该城市这30天空气质量指数

(2)设“在本月30天中随机抽取一天,该天经济损失
由

根据表格数据得共有9+4=13天
所以 
知识点
对某校高一年级学生参加社区服务次数进行统计,随机抽取


(1)求出表中M、p及图中a的值;
(2)若该校高一学生有360人,试估计他们参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[20,25)内的概率。
正确答案
(1)M=40,a=0.125,p=0.075
(2)225
(3)
解析
(1)由题可知



又 



则

(2)参加在社区服务次数在区间

(3)在样本中,处于








知识点
近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康,其形成与


某环保部门为了了解甲、乙两市的空气质量状况,在某月中分别随机抽取了甲、乙两市6天的
(1)求甲、乙两市
(2)若从甲市这6天的样本数据中随机抽取两天的数据,求恰有一天空气质量等级为一级的概率。
正确答案
见解析
解析
(1)甲市抽取的样本数据分别是32,34,45,56,63,70;乙市抽取的样本数据为33,46,47,51,64,71.


因为
(2)由茎叶图知,甲市6天中有2天空气质量等级为一级,有4天空气质量等级为二级,空气质量等级为二级的4天数据为


记“恰有一天空气质量等级为一级”为事件A,则事件A包含的基本事件为:
所以

知识点
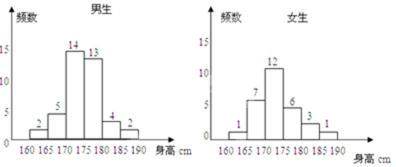
18.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3) 从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析