古典概型与几何概型
共333题

古典概型与几何概型
共333题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设不等式组表示的平面区域为，在区域内随机取一个点，则此点到直线的距离大于2的概率是（）

正确答案

解析

略

知识点

与长度、角度有关的几何概型

题型：填空题

填空题 · 5 分

在区间上随机取一实数，则该实数满足不等式的概率为　。

正确答案

解析

由不等式，可得，所以所求概率为。

知识点

与长度、角度有关的几何概型

题型：填空题

填空题 · 5 分

在区间上随机取两个实数，,则事件“”的概率为_________。

正确答案

解析

略

知识点

与长度、角度有关的几何概型

题型：单选题

单选题 · 5 分

在线段AB上任取一点P，以P为顶点，B为焦点作抛物线，则该抛物线的准线与线段AB有交点的概率是（）

正确答案

解析

略

知识点

与长度、角度有关的几何概型

题型：填空题

填空题 · 5 分

在区间上随机取两个实数，,则事件“”的概率为_________。

正确答案

解析

略

知识点

与长度、角度有关的几何概型

题型：填空题

填空题 · 5 分

15的展开式中各项系数和是 ·

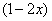
正确答案

-1

解析

略

知识点

与长度、角度有关的几何概型

题型：简答题

简答题 · 12 分

沙糖桔是柑桔类的名优品种，因其味甜如砂糖故名.某果农选取一片山地种植沙糖桔，收获时，该果农随机选取果树20株作为样本测量它们每一株的果实产量（单位：kg），获得的所有数据按照区间进行分组，得到频率分布直方图如图3.已知样本中产量在区间上的果树株数是产量在区间上的果树株数的倍。

（1）求,的值；

（2）从样本中产量在区间上的果树随机抽取两株，求产量在区间

上的果树至少有一株被抽中的概率.

正确答案

见解析。

解析

（1）解:样本中产量在区间上的果树有（株），

样本中产量在区间上的果树有（株），

依题意，有，即.①

根据频率分布直方图可知， ②

解①②得:.

（2）解：样本中产量在区间上的果树有株，分别记为

，

产量在区间上的果树有株，分别记为.

从这株果树中随机抽取两株共有15种情况：，

，.

其中产量在上的果树至少有一株共有9种情况：

，.

记“从样本中产量在区间上的果树随机抽取两株，产量在区间上的

果树至少有一株被抽中”为事件，则.

知识点

与长度、角度有关的几何概型频率分布直方图

题型：填空题

填空题 · 4 分

已知圆C：，直线l：则圆C上任一点到直线l的距离小于2的概率为 .

正确答案

解析

圆的半径为，圆心到直线的距离，要使圆C上任一点到直线l的距离小于2，则此时圆心到直线的距离为3.此时圆上的点位于弧BC上。因为,，所以，所以.所以弧BC的长度为，所以由几何概型得所求概率为.

知识点

点到直线的距离公式直线与圆的位置关系与长度、角度有关的几何概型

题型：单选题

单选题 · 5 分

若命题“或”与命题“非”都是真命题，则

A命题不一定是假命题

B命题一定是真命题

C命题不一定是真命题

D命题与命题同真同假

正确答案

解析

由题可知“非”是真命题，所以是假命题，又因为“或”是真命题，所以是真命题。

知识点

与长度、角度有关的几何概型

题型：简答题

简答题 · 12 分

已知常数且，数列的前项和，数列满足且。

(1)求证：数列是等比数列；

(2)若对于在区间[0，1]上的任意实数，总存在不小于2的自然数，当时，恒成立，求的最小值。

正确答案

见解析。

解析

(1)当时，，整理得，（3分）

由，得，则恒有，从而，所以数列为等比数列，（6分）

(2)由(1)知，则，

所以，（8分）

所以，则在时恒成立。

记，由题意知，，解得或，（11分）

又，所以，综上可知，的最小值为4，（12分）

知识点

与长度、角度有关的几何概型

继续学习学习下一知识点

下一知识点 : 统计与统计案例

百度题库 > 高考 > 文科数学 > 古典概型与几何概型

扫码查看完整答案与解析