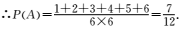- 古典概型与几何概型
- 共333题
4.某次体检,5位同学的身高(单位:米)分别为1.72,1.78,1.80,1.69,1.76,则这组数据的中位数是______(米).
正确答案
1.76
知识点
9.设函数f(x)=-x+2,x∈[-5,5]。若从区间[-5,5]内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
正确答案
解析
依题意,由f(x)≤0,即-x+2≤0,可得x≥2.又因为x∈[-5,5],所以从区间[-5,5]内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率P=
知识点
8.连掷两次骰子得到的点数分别为m和n,记向量a=(m,n)与向量b=(1,-1)的夹角为θ,则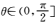
正确答案
解析
知识点
10.如图,给定两个向量






正确答案
解析
过点C分别作OB,OA的平行线,分别交OA,OB于点D、E
设圆的半径为1,在△OCD中,OD=x,CD=y
∠ODC=60°,∠DOC=α,α∈(0°,120°)
由正弦定理得


故x+y=
又由x+y≥

由几何概型的概率公式,得x+y≥


知识点
9.设函数f(x)=-x+2,x∈[-5,5].若从区间[-5,5]内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
正确答案
解析
依题意,由f(x)≤0,即-x+2≤0,可得x≥2.又因为x∈[-5,5],所以从区间[-5,5]内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率P=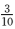
知识点
10.甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中a,b∈{1,2,3,4,5,6},若|a-b|≤1,就称甲乙“心相近”.现任意找两人玩这个游戏,则他们“心相近”的概率为( )
正确答案
解析
试验包含的所有事件共有6×6=36种.
其中满足题设条件的有如下情况:
若a=1,则b=1,2;
若a=2,则b=1,2,3;
若a=3,则b=2,3,4;
若a=4,则b=3,4,5;
若a=5,则b=4,5,6;
若a=6,则b=5,6,共16种.
故他们“心相近”的概率为P=
知识点
4. 设实数

有实根的概率为( )
正确答案
解析
因为
所以
解得
记事件A:P在[0,5]上随机地取值,
关于x的方程
由方程
所以
考查方向
解题思路
先求出p的取值范围,然后用几何概型求概率
易错点
不用几何概型建模
知识点
8.在区间[一1,1]上随机取一个数x,使cos

正确答案
解析
由






考查方向
解题思路
1.先根据



2.根据几何概型的概率公式求出所求的概率。
易错点
由cos

知识点
10.已知圆C:


正确答案
解析
如图,
设与直线






考查方向
解题思路
先要找到圆上哪一部分点到直线
易错点
本题容易因为不理解几何概型的角度模型而导致错误的产生。
知识点
17.已知
(1)若
(2)若
正确答案
(1)
(2)
解析
本题属于利用古典概型、几何概型求概率问题,掌握相关知识点,即可解决问题,解析如下:
解:(1)设

所以所有
为


即
设



所以

所以
即可即
即可上面基本事件中,
符合


所以


如右图
所以




设为
解得




可解得


所以,由几何概型可知:
考查方向
本题考查了古典概型、几何概型与直线方程等方面的知识。
易错点
基本时间空间求错导致出错。
知识点
扫码查看完整答案与解析