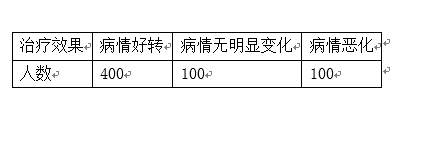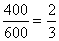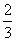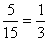- 古典概型与几何概型
- 共333题
某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友,每位朋友1本,则不同的赠送方法共有( )
正确答案
解析
知识点
某药厂测试一种新药的疗效,随机选择600名志愿者服用此药,结果如下:
(1)若另有一病人服用此药,请估计该病人病情好转的概率;
(2)现从服用此药的600名志愿者中选择6人作进一步数据分析,若在三种疗效的志愿者中各取2人,这种抽样是否合理?若不合理,应该如何抽样?(请写出具体人数安排)
(3)在选出作进一步数据分析的6人中,任意抽取2人参加药品发布会,求抽取的2人中有病情恶化的志愿者的概率。
正确答案
见解析。
解析
(1)由已知统计表可知在600个病人中,服药后出现病情好转的频率为
所以估计另一个病人服用此药病情好转的概率为
(2)在三种疗效的志愿者中各取2人,这种抽样不合理
由于用药后人治疗效果之间存在明显差异,所以要进一步抽样则应该按照治疗效果进行分层抽样…,即从病情好转的志愿者中抽4人,从病情无明显变化的志愿者中抽1人,从病情恶化的志愿者中抽1人组成6人样本
(3)将6人中病情恶化的1人用符号A代替,其余5人用分别用符号1,2,3,4,5代替
则从6人中任意抽取2人的基本事件表示如下:(1,2),(1,3),(1,4),(1,5),
(1,A),(2,3),(2,4),(2,5),(2,A),(3,4),(3,5),(3,A),(4,5),
(4,A),(5,A)……10分,一共15个基本事件
其中抽到病情恶化志愿者的基本事件为:(1,A),(2,A),(3,A),(4,A),(5,A)一共5个基本事件
每个基本事件是等可能的……13分,根据古典概型可得,抽取的2人中有病情恶化的志愿者的概率为
知识点
(x+1)9的展开式中x3的系数是________,(用数字作答)
正确答案
84
解析
本题主要考查二项展开式通项的应用. (x+1)9的展开式通项为Tr+1=Cx9-r,所以x3的系数是C=
知识点
本着健康、低碳的生活理念,租自行车骑游的人越来越多,某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费2元(不足1小时的部分按1小时计算),有甲、乙两人相互独立来该租车点租车骑游(各租一车一次),设甲、乙不超过两小时还车的概率分别为,;两小时以上且不超过三小时还车的概率分别为,;两人租车时间都不会超过四小时。
(1)求甲、乙两人所付的租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量ξ,求ξ的分布列及数学期望Eξ.
正确答案
见解析。
解析
甲、乙两人所付的租车费用之和ξ的分布列为
知识点
某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查.调查问卷共10道题,答题情况如下表:
(1)如果出租车司机答对题目数大于等于9,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(2)从答对题目数少于8的出租车司机中任选出两人做进一步的调查,求选出的两人中至少有一名女出租车司机的概率。
正确答案
(1)0.45
(2)0.7
解析
(1)答对题目数小于9道的人数为55人,记“答对题目数大于等于9道”为事件A

(2)设答对题目数少于8道的司机为 A、B、C、D、E,其中A、B为女司机 ,选出两人包含AB、AC、AD、AE、BC、BD、BE、CD、CE、DE共10种情况,至少有1名女驾驶员的事件为AB、AC、AD、AE、BC、BD、BE共7种。
记“随机选出的两人中至少有1名女驾驶员”为事件M,则

知识点
某市公租房的房源位于A、B、C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的4位申请人中:
(1)没有人申请A片区房源的概率;
(2)每个片区的房源都有人申请的概率。
正确答案
见解析。
解析
这是等可能性事件的概率计算问题。
知识点

(2)求甲、乙两人所付的租车费用之和小于6元的概率。
正确答案
见解析。
解析
知识点
某单位
的年龄在25岁至50岁之间,按年龄分组:第1组





如图5所示,下表是年龄的频率分布表。
(1)求正整数


(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人在第3组的概率。
正确答案
见解析。
解析
解:(1)由频率分布直方图可知,

所以
且
总人数
(2)因为第1,2,3组共有25+25+100=150人,利用分层抽样在150名员工中抽取
第1组的人数为
第2组的人数为
第3组的人数为
所以第1,2,3组分别抽取1人,1人,4人,
(3)由(2)可设第1组的1人为


















其中恰有1人年龄在第3组的所有结果为:








所以恰有1人年龄在第3组的概率为
知识点
(1+2x)6的展开式中x4的系数是______。
正确答案
240
解析
∵(1+2x)6的展开式中含x4的项为
知识点
2012年春节联欢晚会中,其中某段节目有6名演员演出,安排6名演员的演出顺序时,要求演员甲不第一个出场,也不最后一个出场,则不同的安排方法种数( )
正确答案
解析
安排第一个出场的演员,共有除甲之外的5种安排方法;再安排最后一个出场的演员,共有剩下的4种安排方法(不含甲和刚安排的第一个);最后4名演员在剩下的4个出场顺序中进行全排列,有

知识点
扫码查看完整答案与解析