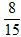- 古典概型与几何概型
- 共333题
空气质量指数

某市






(1)估计该城市一个月内空气质量类别为优的概率;
(2)从空气质量级别为三级和四级的数据中任取2个,
求恰好有一天空气质量类别为中度污染的概率。
正确答案
见解析。
解析
(1)由条形统计图可知,空气质量类别为优的天数为8天,
所以此次监测结果中空气质量类别为优的概率为
(2)样本中空气质量级别为三级的有4天,设其编号为
样本中空气质量级别为四级的有2天,设其编号为
则基本事件有:




其中恰好有1天空气质量类别为中度污染的情况为:

所以恰好有1天空气质量类别为中度污染的概率为
知识点
一枚硬币连掷5次,则至少一次正面向上的概率是
正确答案
解析
略
知识点
一名学生在军训中练习射击项目,他射击一次,命中目标的概率是
(1)求这名学生在第3次射击时,首次命中目标的概率;
(2)求这名学生在射击过程中,恰好命中目标3次的概率。
正确答案
(1)
(2)
解析
(1)这名学生第一、二次射击未中目标,第三次击中目标的概率为
P1 =
(2)这名学生恰好击中目标3次的概率为
P2 =
知识点
某公司有男职员45名,女职员15名,按照分层抽样的方法组建了一个4人的科研攻关小组。
(1)求某职员被抽到的概率及科研攻关小组中男、女职员的人数;
(2)经过一个月的学习、讨论,这个科研攻关组决定选出两名职员做某项实验,方法是先从小组里选出1名职员做实验,该职员做完后,再从小组内剩下的职员中选一名做实验,求选出的两名职员中恰有一名女职员的概率;
(3)试验结束后,第一次做试验的职员得到的试验数据为68,70,71,72,74,第二次做试验的职员得到的试验数据为69,70,70,72,74,请问哪位职员的实验更稳定?并说明理由。
正确答案
见解析。
解析
(1)

设有



(2)把







(3)

第二次做试验的职员做的实验更稳定………………………12分
知识点
在某大学自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级. 某考场考生的两科考试成绩的数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.
(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求该考场考生“数学与逻辑”科目的平均分;
(3)已知参加本考场测试的考生中,恰有两人的两科成绩均为A. 在至少一科成绩为A的考生中,随机抽取两人进行访谈,求这两人的两科成绩均为A的概率。
正确答案
(1)3
(2)2.9
(3)
解析
(1)因为“数学与逻辑”科目中成绩等级为B的考生有10人,
所以该考场有
所以该考场考生中“阅读与表达”科目中成绩等级为A的人数为
(2)求该考场考生“数学与逻辑”科目的平均分为

(3)因为两科考试中,共有6人得分等级为A,又恰有两人的两科成绩等级均为A,
所以还有2人只有一个科目得分为A………………9分
设这四人为甲,乙,丙,丁,其中甲,乙是两科成绩都是A的同学,则在至少一科成绩等级为A的考生中,随机抽取两人进行访谈,基本事件空间为


设“随机抽取两人进行访谈,这两人的两科成绩等级均为A”为事件B,所以事件B中包含的基本事件有1个,则
知识点
从某批产品中,有放回地抽取产品2次,每次随机抽取1件,假设事件
(1)求从该批产品中任取1件是二等品的概率P;
(2)若该批产品共100件,从中一次性任意抽取2件,求事件
正确答案
见解析。
解析
(1)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件是二等品”。
则A0、A1互斥,且A=A0+A1,
故P (A)=P (A0+A1)=P (A0) +P (A1)=(1-p)2+C
依题意,知1-p2=0.96,
又p>0,得p=0.2。
(2)若该批产品共100件,由(1)知,其中共有二等品100×0.2=20件。
记C表示事件“取出的2件产品中无二等品”,
则事件B与事件C互斥,依题意,知
P(C)=

知识点
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物. PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
石景山古城地区2013年2月6日至15日每天的PM2.5监测数据如茎叶图所示。
(1)计算这10天PM2.5数据的平均值并判断其是否超标;
(2)小陈在此期间的某天曾经来此地旅游,求当天PM2.5日均监测数据未超标的概率;
(3)小王在此期间也有两天经过此地,这两天此地PM2.5监测数据均未超标.请计算出这两天空气质量恰好有一天为一级的概率。
正确答案
(1)未超标(2)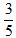
解析
(1)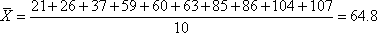
且64.8在35与75之间,空气质量属于二级,未超标. …………3分
(2)记“当天PM2.5日均监测数据未超标”为事件A,
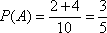
(3)由茎叶图知PM2.5数据在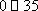

从这六个数据中,任意抽取2个的结果有:
(21,37),(21,59),(21 ,60),(21,63),
(26,37),(26,59),(26 ,60),(26,63),
(21,26),(37,59),(37 ,60),(37,63),
(59,60),(59,63),(60 ,63) , 共有15个. …………10分
记“这两天此地PM2.5监测数据均未超标且空气质量恰好有一天为一级” 为事件B, 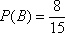
知识点
某中学在高三年级开设了





(1)求

(2)若从

正确答案
见解析。
解析
知识点
盒中有10只螺丝钉,其中有3只是坏的,现从盒中随机地抽取4只螺丝钉,那么
正确答案
解析
恰有1只坏的概率为P1 =




知识点
从5名女生和2名男生中任选3人参加英语演讲比赛,设随机变量
(1)求
(2)求
(3)求“所选3人中男生人数
正确答案
见解析。
解析
(1)
P(

所以
(2)由(1)得
E



(3)由(1)知“所选3人中男生人数
P (





知识点
扫码查看完整答案与解析