- 三角函数的综合应用
- 共200题
6.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在锐角
(1)求角
(2)若

正确答案
(1)由

(2)
又
解析
解析已在路上飞奔,马上就到!
知识点
21.过椭圆C:


(1) 若

(2) 求证:点B为一定点
正确答案
证明:(1)连结

则在

由内角平分线定理可知:
而



则



于是有:

(2)设过A(m,0)的直线l与椭圆C:






PQ直线方程:

而

下面利用分析法证明:
即证:
只需证:
只需证:
即证:
而(


同理
由③×④可知②成立,从而①式得证。因此

∴点B为一定点(
另法:证(1)设直线l过A(m,0)与椭圆交于
而



∴


(2)由

由


由①×②得 
又

∵




由③⑥可知 

∴点B为一定点(
解析
解析已在路上飞奔,马上就到!
知识点
6.用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,该长方体的最大体积是________
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
12.在半径为R的圆周上任取A、B、C三点,试问三角形ABC为锐角三角形的概率( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)求曲线

(2)若函数

(3)当
正确答案
解:(1)因为
所以曲线

(2)





所以

x=1时,

(3)当
即证:
即证:
构造函数:
当
所以
又
即
所以
解析
解析已在路上飞奔,马上就到!
知识点
11.命题“存在

正确答案
任意
解析
解析已在路上飞奔,马上就到!
知识点
15.若函数y=ex-a(e为自然常数)的图象上存在点(x,y)满足约束条件
正确答案
解析
作可行域如图中阴影部分所示
再平移y=ex-a的图像与区域相交,可知在点(0,0)处
y=ex-a与
在点(5,-1)处得a的最大值为
故实数a的取值范围是
考查方向
解题思路
1、根据不等式组画平面区域,并画出函数y=ex-a的图像。
2、平移y=ex-a的图像与区域相交,从而找出最优解,并代入得到a的范围。
易错点
1、本题易在根据不等式组画平面区域时出错。
2、本题容易忽视“-a” 中的“-”而出错。
知识点
10.已知

正确答案
解析

所以
考查方向
本题主要考查三角函数的基本性质,诱导公式,两角和与差三角函数,三角函数的恒等变换,考查运算能力,难度中等.
解题思路
本题主要考查三角函数的基本性质,诱导公式,两角和与差三角函数,三角函数的恒等变换.
解题步骤如下:把未知角变换成已经角。利用诱导公式和同角三角函数的基本关系式求解。
易错点
本题不容易想到角的变换,有时公式记错,导致结果错误。
知识点
3.右图所示的程序运行后输出的结果是()
正确答案
解析
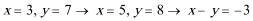
考查方向
解题思路
分条件不断赋值即可
易错点
1、本题易在认识条件语句时出错。
2、本题在赋值时,易在程序先后顺序上出错。
知识点
扫码查看完整答案与解析









































