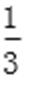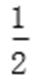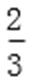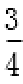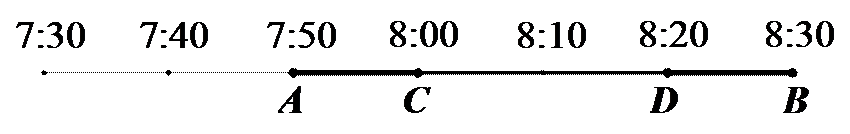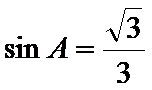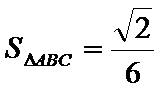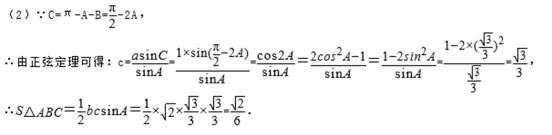- 三角函数的综合应用
- 共200题
4.某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是
正确答案
解析
试题分析:如图所示,画出时间轴:
小明到达的时间会随机落在途中线段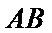
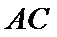
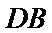
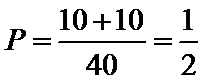
考查方向
解题思路
先确定几何度量,再根据几何概型的概率计算公式即可求解。
易错点
不能准确选择几何度量导致出错。
知识点
6.如图,某几


正确答案
解析
试题分析:该几何体直观图如图所示:
是一个球被切掉左上角的





考查方向
解题思路
由三视图可知该几何体的直观图如右图所示,则多面体的体积可求出。
易错点
不能将三视图还原为原图导致出错。
知识点

17.求C;
18.若


正确答案
解析
试题分析:本题属于正余弦定理的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由正弦定理得:
∵
∴
∴
∵
∴
考查方向
解题思路
先利用正弦定理进行边角代换化简得得

易错点
相关知识点不熟容易处错。
正确答案
解析
试题分析:本题属于正余弦定理的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由余弦定理得:
∴
∴
∴
考查方向
解题思路
根据






易错点
相关知识点不熟容易处错。
11.cos2

正确答案
解析
由二倍角公式得
考查方向
解题思路
这是一个来自于课本的题,直接利用课本公式解题,这告诉我们一定要立足于课本.有许多

易错点
本题考查了三角函数二倍角公式,二倍角公式的记忆可能发生错误
知识点
14.函数

单位长度得到.
正确答案
解析
因为





考查方向
解题思路
先根据和角公式化简函数,再根据图像变换分析平移量。
易错点
平移的单位数量问题,要注意是否先进行了周期变换。
知识点
已知函数f(x)=4tanxsin(


15.求f(x)的定义域与最小正周期;
16.讨论f(x)在区间[
正确答案
(Ⅰ)
解析
本题属于三角恒等变换与函数性质的综合应用问题,属于简单题,选用恰当的公式,是解决三角问题的关键




所以, 
考查方向
解题思路
(Ⅰ)先利用诱导公式、两角差余弦公式、二倍角公式、配角公式将函数化为基本三角函数:
易错点
化简函数解析式时容易出错。
正确答案
(Ⅱ)在区间

解析
本题属于三角恒等变换与函数性质的综合应用问题,属于简单题,选用恰当的公式,是解决三角问题的关键



由
设

所以, 当



考查方向
解题思路


易错点
化简函数解析式时容易出错。
2.
正确答案
解析
原式=


考查方向
易错点
本题主要考查诱导公式与两角和与差的正余弦公式列在应用公式变形时容易出错。【解题思路】三角函数公式题也是每年高考必考内容,一般以客观题形式出现,属得分题.本题需要把公式进行变形,变得与两角和的正弦公式即可。
知识点
6、点G为△ABC的重心(三角形三边中线的交点G,设
正确答案
解析
点G为△ABC的重心,所以
选择答案D。
考查方向
解题思路
利用重心的性质和利用基底向量表示即可。
易错点
方向和符号问题。
知识点
∆ABC中,D是BC上的点,AD平分∠BAC,∆ABD是∆ADC面积的2倍。
17.求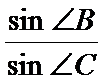
18.若AD=1,DC=
正确答案
正确答案
在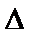
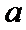
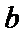
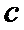
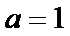
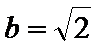
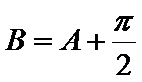
17.求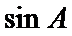
18.求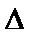
正确答案
解析
考查方向
解题思路
由已知可得A为锐角,由正弦定理,两边平方整理可解得sinA的值.
易错点
诱导公式的符号问题。
正确答案
解析
考查方向
解题思路
利用三角形内角和定理可求C,由正弦定理可得c,根据三角形面积公式即可得解.
易错点
诱导公式的符号问题。
扫码查看完整答案与解析