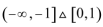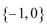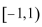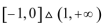- 三角函数的综合应用
- 共200题
17.如果函数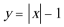
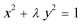
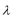
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知抛物线










(Ⅰ)求抛物线
(Ⅱ)当


(Ⅲ)若直线



正确答案
解:(1)∵点

∴


(2)法一:∵当



设


∴ 


法二:∵当


∴


∴直线


得



同理可得


(3)法一:设


直线

直线

∴

∴直线



∵



法二:设点


以


⊙

①-②得:直线

当



∵



解析
解析已在路上飞奔,马上就到!
知识点
6. 将函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 如图,四棱锥






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若n展开式的二项式系数之和为256,则n=______,其展开式的常数项等于_____.(用数字作答)
正确答案
8,70
解析
解析已在路上飞奔,马上就到!
知识点
11.《九章算术》之后,人们进一步用等差数列求和公式来解决更多

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知点A(-1,1),点B(2,y),向量a=(l,2),若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数

(1)求
(2)设不等式




(3)已知






正确答案
(1)
由



(2)

由

令

又

(3)设存在公差为









故
②-①×2得,

故



解析
解析已在路上飞奔,马上就到!
知识点
16.定义一个对应法则







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析