- 几何证明选讲
- 共247题
设函数f(x)=emx+x2-mx.
25.证明:f(x)在(-∞,0)单调递减,在(0,+∞)单调递增;
26.若对于任意x1, x2∈[-1,1],都有|f(x1)- f(x2)|≤e-1,求m的取值范围
正确答案
正确答案
选修4-1:几何证明选讲
如图,






28.求证:
29.求证:
正确答案
详见解题过程;
解析
试题分析:本题属于平面几何的基本问题,由圆的性质直接导出角关系。∵




考查方向
解题思路

易错点
对图形的分析不到位和定理不熟练导致出错。
正确答案
详见解题过程
解析
试题分析:本题属于平面几何的基本问题,由相似关系去证所证。连接





考查方向
解题思路

易错点
对图形的分析不到位和定理不熟练导致出错。
如图,








27.求证:
28.若

正确答案
见解析
解析

考查方向
解题思路
利用同弧等角定理,和三角形全等的条件,即可得到相关的结论。
易错点
不容易找到辅助线。
正确答案


解析
已知






考查方向
解题思路
利用同弧等角定理,和三角形全等的条件,即可得到相关的结论。
易错点
不容易找到辅助线。
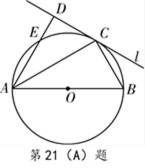
如图,圆O的直径AB=4,C为圆周上一点,BC=2,过C作圆O的切线l,过A作l的垂线AD,AD分别与直线l、圆O交于点D、E,求线段AE的长。
正确答案
见解析
解析
在Rt△ABC中,因为AB=4,BC=2,所以∠ABC=60°,
因为l为过C的切线,所以∠DCA=∠CBA,
所以∠DCA=∠ABC=60°,
又因为AD⊥DC,所以∠DAC=30°。
在△AOE中,因为∠EAO=∠DAC+∠CAB=60°,且OE=OA,
所以AE=AO=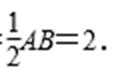
知识点
如图,AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB的延长线于点C,若DA = DC,求证:AB = 2 BC。
正确答案
见解析。
解析
连结OD,BD,
因为AB是圆O的直径,所以
因为DC是圆O的切线,所以
因为AD = DC,所以

即2OB = OB + BC,得OB = BC,故AB = 2 BC。
知识点
如图,M是平行四边形ABCD的边AB的中点,直线l过点M分别交AD,AC于点E,F,若AD=3AE,则AF:FC= 。
正确答案
1:4
解析
如图所示,设直线l交CD的延长线于点N。
∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD。
∵M是边AB的中点,∴
∴

故答案为1:4。
知识点
如图,⊙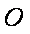
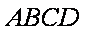


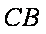
长线上一点,直线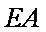
求证: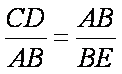
正确答案
见解析。
解析
连结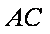
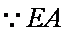
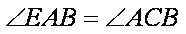
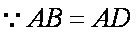
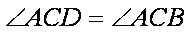
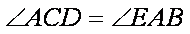

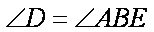
∴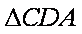
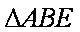
∴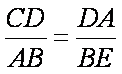
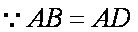
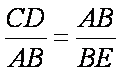
知识点
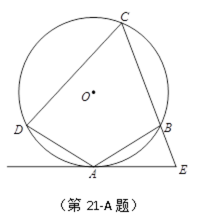
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB。
(1)证明:AC2=AD·AE
(2)证明:FG∥AC
正确答案
见解析。
解析
(1)∵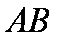

∴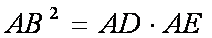
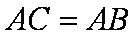
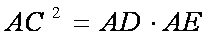
(2)∵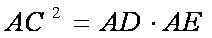
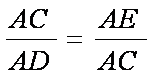

∴
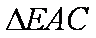
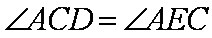
又∵四边形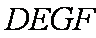

∴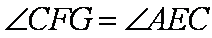
∴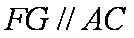
知识点
如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F。
(1)若AC=6,AB=10,求⊙O的半径;
(2)连接OE、ED、DF、EF,若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由。
正确答案
见解析。
解析
(1)连接OD. 设⊙O的半径为r.
∵BC切⊙O于点D,∴OD⊥BC.
∵∠C=90°,∴OD∥AC,∴△OBD∽△ABC.
∴


∴⊙O的半径为
(2)结论:四边形OFDE是菱形.
证明:∵四边形BDEF是平行四边形,∴∠DEF=∠B.
∵∠ODB=90°,∴∠DOB+∠B=90°,∴∠DOB=60°.
∵DE∥AB,∴∠ODE=60°。∵OD=OE,∴△ODE是等边三角形.
∴OD=DE.∵OD=OF,∴DE=OF.∴四边形OFDE是平行四边形.
∵OE=OF,∴平行四边形OFDE是菱形.
知识点
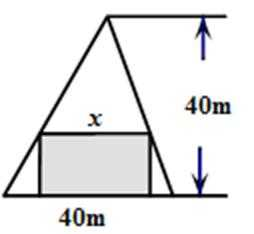
13.在如图所示的锐角三角形空地中, 欲建一个面积不小于300m2的内接矩形花园(阴影部分), 则其边长x(单位m)的取值范围是__________.
正确答案
[10,30]
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析