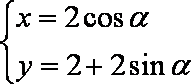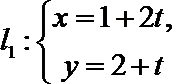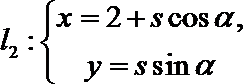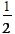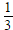- 坐标系与参数方程
- 共275题
极坐标系下,直线

正确答案
1
解析
解:直线



圆

圆心到直线的距离等于

故直线和圆相切,
故答案为1。
知识点
函数

正确答案
解析
分段函数在x=3处不是无限靠近同一个值,故不存在极限.
知识点
如图,平面直角坐标系中,射线











(1)用


(2)用


(3)写出四边形



正确答案
见解析
解析
(1)
∴
(2)
∴
(3)
∴
∴


∴

又

∴



知识点


正确答案
36
解析
略
知识点
二项式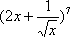

正确答案
280
解析
略
知识点
从极点O作射线,交直线

正确答案
见解析。
解析
设




化为平面直角坐标系的方程为


因为有且只有一个点




知识点
选修4—4:极坐标与参数方程
在直角坐标系xOy 中,曲线C1的参数方程为
(
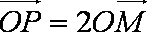
(1)求C2的方程;
(2)在以O为极点,x 轴的正半轴为极轴的极坐标系中,射线
正确答案
见解析。
解析
(1)设P(x,y),则由条件知M(
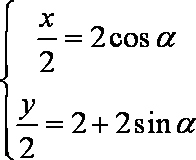
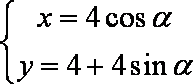
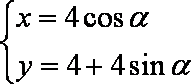

(2)曲线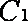
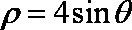
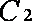
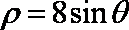
射线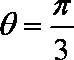
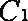
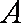
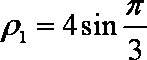
射线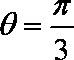
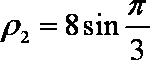
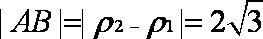
知识点
选修4-4:坐标系与参数方程
(1) 以直角坐标系的原点为极点,


(2)已知极点与原点重合,极轴与x轴正半轴重合,若直线C1的极坐标方程为:


正确答案
见解析。
解析
(1)直线和圆的直角坐标方程分别为
则圆心为C(1,2),半径R= 
从而C到直线y=x的距离d=
由垂径定理得,|AB|=
(2)解:曲线C1可化为:
曲线C2是以(1,3)为圆心,1为半径的圆………………………6分
(1,3)关于直线

知识点
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4—1:几何证明选讲
如图,AB是

(1)求证:FG//AC;
(2)若CG=1,CD=4,求
23.选修4-4:极坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程为

(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(3,
24.选修4-5:不等式选讲
(1)求不等式
(2)已知
22.选修4—1:几何证明选讲
如图,AB是

(1)求证:FG//AC;
(2)若CG=1,CD=4,求
23.选修4-4:极坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程为(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2sin θ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(3,),求|PA|+|PB|.
24.选修4-5:不等式选讲
(1)求不等式
(2)已知

正确答案
正确答案
正确答案
选做题(14 ~ 15题,只能从中选做一题)
14. (坐标系与参数方程选做题)
直线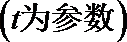
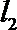
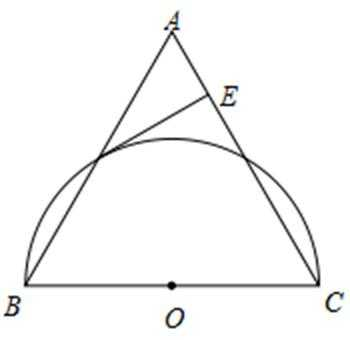
15.(几何证明选讲选做题)
如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,
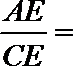
正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析