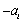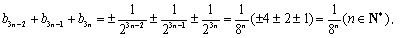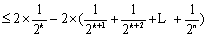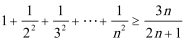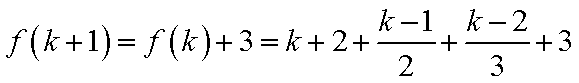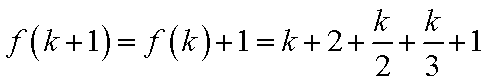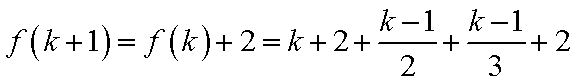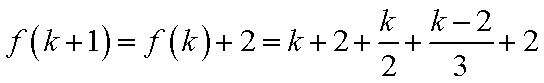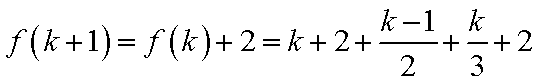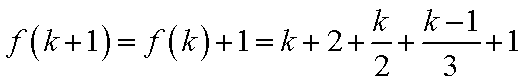- 推理与证明
- 共88题
21.(1) [选修4-2:矩阵与变换]
已知



(1)求矩阵
(2)若矩阵
正确答案
见解析
解析
解:(1)
(2)
考查方向
解题思路
1利用已知条件求矩阵A,2由矩阵A,求矩阵A-1,3由矩阵A-1,矩阵
易错点
本题必须注意审题,否则求解错误。
知识点
21.数列

(1)证明:“对任意


(2)若







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知△ABC的三边长为a、b、c,若
正确答案
(用反证法证明1)
∵


∴
∴b2≤ac 即ac-b2≥0.
假设B是钝角,则cosB<0,
由余弦定理可得,

这与cosB<0矛盾,故假设不成立.
∴B不可能是钝角.
(用反证法证明2)
∵


∴
假设B是钝角,则
则B是△ABC的最大内角,所以b>a,b>c,
(在三角形中,大角对大边),
从而

故假设不成立,因此B不可能是钝角.
(用综合法证明)
∵


∴
证明:∵


∴
由余弦定理和基本不等式可得,

∵a,b,c为△ABC三边,∴a+c>b,
∴
∴cosB>0,
∴∠B<900,因此B不可能是钝角.
解析
解析已在路上飞奔,马上就到!
知识点
20.已知


正确答案
(反证法)假设

设




由上述矛盾可知,
解析
解析已在路上飞奔,马上就到!
知识点
对于数列
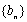
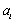
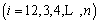
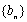
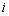
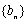
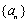
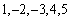
已知数列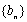
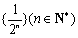
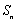
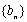
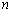
(1)写出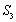
(2)若生成数列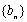
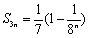
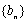
(3)证明:对于给定的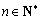
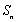
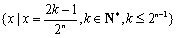
正确答案
见解析
解析
(1)由已知,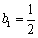
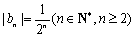
∴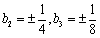
由于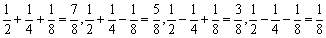
∴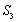
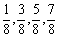
(2)∵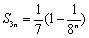
当
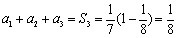
当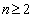
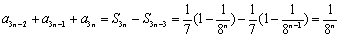
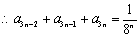
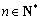
∵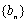
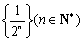
∴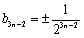
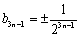
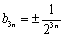
∴
在以上各种组合中,
当且仅当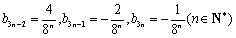
∴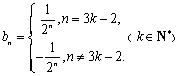
(3)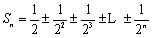
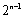
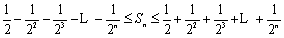
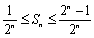
又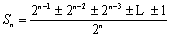
满足条件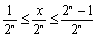
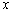
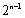
设数列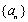
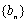
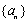
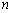
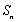
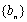
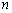
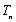
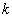
由于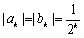
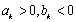
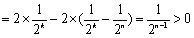
所以,只有当数列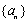
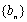
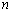
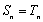
∴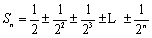
∴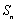
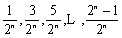
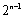
即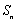
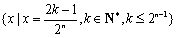
知识点
若函数


(1)判断下列函数:①

(2)证明:对任意的正奇数

(3)证明:任意的

正确答案
见解析
解析
(1)①②都是等比源函数.
(2)证明:假设存在正整数




等式两边同除以

因为
所以等式
所以假设不成立,说明对任意的正奇数

(3)因为任意的

所以任意的



由



令

所以
所以任意的


所以任意的

知识点
已知△ABC的三边长都是有理数。
(1)求证cosA是有理数;
(2)求证:对任意正整数n,cosnA是有理数。
正确答案
见解析。
解析
(方法一)(1)证明:设三边长分别为




∴
(2)①当
当


②假设当

当



解得:
∵cosA,


∴
即当
综上所述,对于任意正整数n,cosnA是有理数。
(方法二)证明:(1)由AB、BC、AC为有理数及余弦定理知

(2)用数学归纳法证明cosnA和
①当


②假设当


当


及①和归纳假设,知

即当
综合①、②可知,对任意正整数n,cosnA是有理数。
知识点
已知函数


(1)证明:函数

(2)求方程
(3)若数列




正确答案
见解析。
解析
解:
(1)由




(2)由(1)得:








解法1:


当







(3)记


(i)当







②假设当








(ii)当







①当








故对任意的

综上所述,存在常数


知识点
21.设数列
(1)当


(2)当

(i)
(ii)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.设集合



(1)求



(2)猜想
正确答案
(1)



(2)猜想
解析
试题分析:本题属于探究性问题,题目的难度是逐渐由易到难,通过归纳猜想,得出结论,再利用数学归纳法进行证明。
(1)



(2)猜想
下用数学归纳法证明之.
证明:①当
②假设当



则当

而当集合






所以

即
所以当
综上所述,猜想成立.
考查方向
解题思路
本题考查数学归纳法,解题步骤如下:
1、验证当n取第一个值

2、假设当
3、由(1)(2)就可以判定,对于一切n≥
易错点
数学归纳法证明的步骤,尤其第二部归纳递推要过程充分。
知识点
23.已知构成某系统的元件能正常工作的概率为p(0<p<1),且各个元件能否正常工作是相互独立的。今有2n(n大于1)个元件可按下图所示的两种联结方式分别构成两个系统甲、乙。
(1)试分别求出系统甲、乙能正常工作的概率p1,p2;
(2)比较p1与p2的大小,并从概率意义上评价两系统的优劣。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.用数学归纳法证明: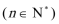
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知集合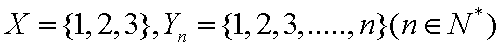

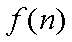
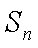
(1)写出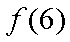
(2)当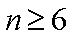
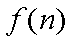
正确答案
(1)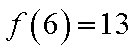
(2)当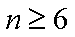
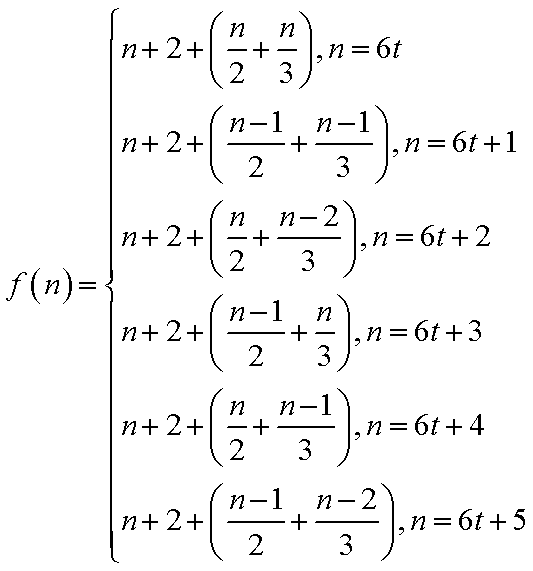
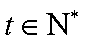
下面用数学归纳法证明:
①当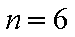
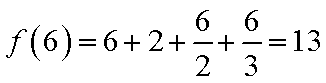
②假设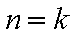
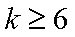
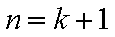
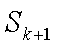
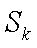
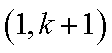
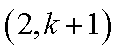
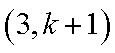
1)若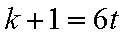
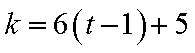
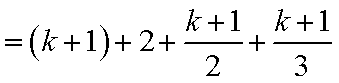
2)若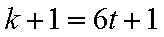
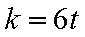
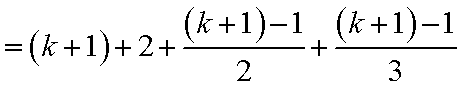
3)若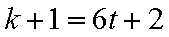
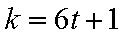
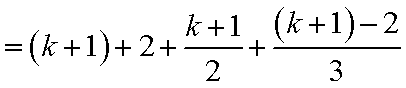
4)若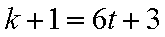
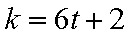
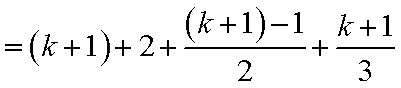
5)若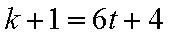
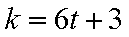
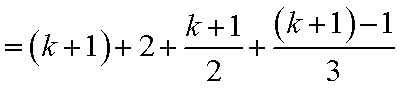
6)若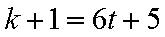
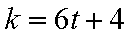
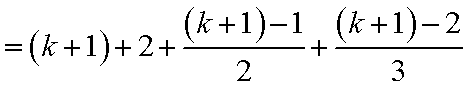
综上所述,结论对满足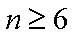
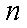
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析