- 选修部分
- 共638题
选修4—1;几何证明选讲.
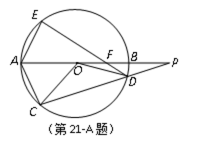
如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.
29.求证:DE2=DB•DA;
30.若DB=2,DF=4,试求CE的长.
正确答案
见解析
解析
证明:连接OF.
因为DF切⊙O于F,所以∠OFD=90°.所以∠OFC+∠CFD=90°.因为OC=OF,所以∠OCF=∠OFC.因为CO⊥AB于O,所以∠OCF+∠CEO=90°.所以∠CFD=∠CEO=
所以DE2=DB•DA.
考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
正确答案
见解析
解析
解:


又由29题可知,DE=DF=4, 


考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
选修4-1:几何证明选讲
已知四边形









28.求证:
29.若

正确答案
详见解析
解析
解:(Ⅰ)由

由角分线定理可知,

考查方向
相似三角形的性质,与圆有关的比例线段
解题思路
将等积式转换成比例式,然后找到三角形,证明三角形相似后,得到等量关系
易错点
找不到证明三角形相似的条件
正确答案
详见解析
解析
∴
又
∴

考查方向
相似三角形的性质,与圆有关的比例线段
解题思路
将等积式转换成比例式,然后找到三角形,证明三角形相似后,得到等量关系。利用等量转换法,证明线段相等
教师点评
此题型要求学生对相似三角形和与圆有关的比例线段有一个准确而又熟练的掌握
11.定积分
正确答案
e
解析


知识点
如图,AB是半圆O的直径,P在AB的延长线上,PD与半圆O相切于点C,AD⊥PD,若PC=4,PB=2,则CD= 。
正确答案
解析
设圆的半径为R,连接OC。
∵ PD与半圆O相切于点C,∴ PC2=PB•PA,OC⊥PD,。
∵ PC=4,PB=2,∴ 42=2×(2+2R),
解得R=3。
又∵ AD⊥PD,∴ OC∥AD。
∴ 
∴ 

知识点
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC, DE交AB于点F,求证:△PDF∽△POC。
正确答案
见解析。
解析
因为AE=AC,∠CDE=∠AOC,
又∠CDE=∠P+∠PFD,∠AOC=∠P+∠OCP,
从而∠PFD=∠OCP。
在△PDF与△POC中,∠P=∠P,∠PFD=OCP,
故 △PDF∽△POC
知识点
设曲线2x2+2xy+y2=1在矩阵A=(
(1)求实数a,b的值。
(2)求A2的逆矩阵。
正确答案
(1)a=1,b=1
(2)A2的逆矩阵为
解析
(1)设曲线2x2+2xy+y2=1上的点(x,y)在矩阵A=(
则(


∵x′2+y′2=1
∴(ax)2+(bx+y)2=1
∴(a2+b2)x2+2bxy+y2=1
∵2x2+2xy+y2=1
∴a2+b2=2,2b=2
∴a=1,b=1
∴A=(
(2)A2=(



∴A2的逆矩阵为
知识点
如图,AB为

(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
正确答案
见解析
解析
证明:(1)由直线CD与
由AB为
从而 ∠EAB+∠EBF=
又EF⊥AB,得∠FEB+∠EBF=
从而∠FEB=∠EAB.
故∠FEB=∠CEB.
(2)BC⊥CE,EF⊥AB,∠FEB=∠CEB,BE是公共边,
得Rt△BCE≌Rt△BFE,所以BC=BF.
类似可证:Rt△ADE≌Rt△AFE,得AD=AF.
又在Rt△AEB中,EF⊥AB,故EF2=AF·BF,
所以EF2=AD·BC.
知识点
选修4-2:矩阵与变换
设



(1)求
(2)求矩阵A的特征值。
正确答案
见解析。
解析
(1)设直线



即 


所以 
即 
所以
所以 
(2)由(1)知矩阵A=
特征矩阵为
特征多项式为
令



知识点
选修4-2:矩阵与变换
如图,矩形





(1)求
(2)判断矩阵
正确答案
见解析。
解析
(1)设
故



(2)因为矩阵MN的特征多项式


知识点
选修4一2:矩阵与变换
若圆


(1)求
(2)判断矩阵


正确答案
见解析。
解析
(1)设点


则
因为点



又圆方程为






(2)

所以
知识点
如图,在






正确答案
解析
略
知识点
A市甲厂因购买B市乙公司的一批木料,与乙公司签订了一份买卖合同,但合同对付款地点和交货地点未加约定,并且未能达成补充协议。下列关于付款地或交货地的表述中,正确的有( )。
A.付款地为A市
B.交货地为A市
C.付款地为B市
D.交货地为B市
正确答案
C,D
解析
[解析] 履行地点不明确的,给付货币的,在接受货币一方所在地履行;交付不动产的,在不动产所在地履行;其他标的在履行义务一方所在地履行。
选修4—1:几何证明选讲.
如图,已知


求证:
(1)
29.
正确答案
见解析
解析
PE切圆O于点E,


∠ECD=∠A+∠CPA
∠EDC=∠BEP+∠DPE


考查方向
考查与圆有关的比例线段问题
解题思路
先证明三角形中两角相等,则对应的两边相等
易错点
在角相等的转化过程中易错。
教师点评
本小问属于中档题,只要认真分析,可以得满分
正确答案
略
解析





同理△PDE
DE=CE
考查方向
本题考查了相似三角形的性质
解题思路
本题通过角的相等,转化为三角形相似,从而得到比例关系
易错点
相似比的转化过程易错
教师点评
本小题第二问较难,必须多角度转化比例关系才能得到结果
已知AB是圆O的直径,C为圆O上一点,CD⊥AB于点D,弦BE与CD、AC 分别交于点M、N,且MN = MC
(1)求证:MN = MB;
(2)求证:OC⊥MN。
正确答案
见解析
解析
(1)连结AE,BC,∵AB是圆O的直径,∴∠AEB=90°,∠ACB=90°∵MN=MC,∴∠MCN=∠MNC又∵∠ENA=∠MNC,∴∠ENA=∠MCN∴∠EAC=∠DCB,∵∠EAC=∠EBC,∴∠MBC=∠MCB,∴MB=MC∴MN=MB, ………5分
(2)设OC∩BE=F,∵OB=OC,∴∠OBC=∠OCB
由(1)知,∠MBC=∠MCB,∴∠DBM=∠FCM,又∵∠DMB=∠FMC
∴∠MDB=∠MFC,即∠MFC=90°∴OC⊥MN, …………10分
知识点
扫码查看完整答案与解析